Summary
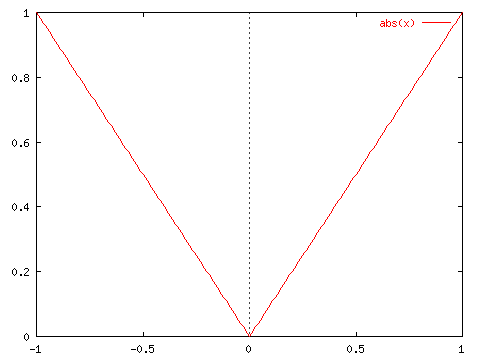
Tangent line: the tangent line to a curve at the point x=a is the line that best approximates the function in the vicinity of a. At some points, no such line exists: for example, a corner in a graph causes real problems,

or a jump discontinuity. Other problems include infinite slopes of tangent lines:
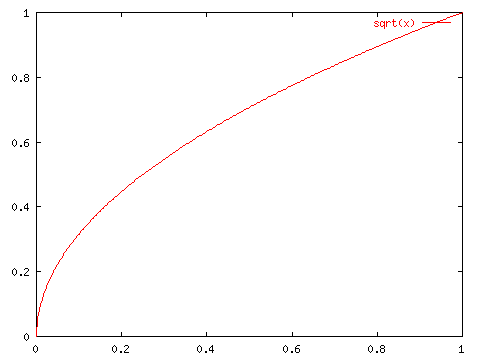
However, for many important cases, if we zoom in on a graph we see that the curve appears closer and closer to a straight line.
Derivative: The derivative of a function f at x is defined as
![]()
provided this limit exists. It represents the slope of the tangent line to the graph of f at x.
The derivative represents the instantaneous rate of change of y with respect to x.
The smoothness of a curve corresponds to whether or not the derivative exists. Continuity corresponds to connectedness; differentiability corresponds to smoothness.
More good news: all these types of functions that we've considered to this point are smooth on their domains: