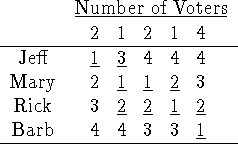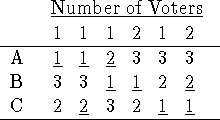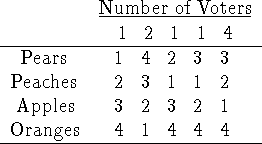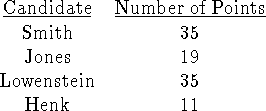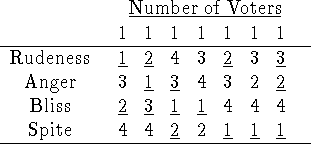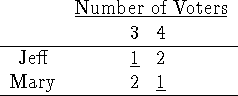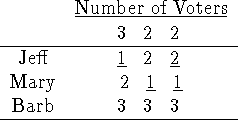

Next: About this document
Name:
Directions: Show your work! Answers without justification will
likely result in few points. Your written work also allows me the option of
giving you partial credit in the event of an incorrect final answer (but good
reasoning). Indicate clearly your answer to each problem (e.g., put a box
around it). Good luck!
Problem 1 (10 pts).
I (8 pts). Below are four terms, followed by six definitions. Choose the
most appropriate definition for each term and place its letter next to the
term.
-
nondictatorship
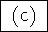
-
universal domain
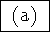
-
Pareto optimality
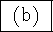
-
independence from irrelevant alternatives
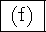
Possible definitions:
-
There is no restriction on the preference-rankings a voter may choose.
-
If all voters prefer candidate A to candidate B, then the group decision will
be to prefer A to B.
-
No single voter totally determines the group choice.
-
All candidates are treated the same way.
-
All ballots are treated the same way.
-
If a group prefers A over B, then introduction of C should not change the group
preference to B over A.
II (2 pts). Describe Arrow's Impossibility Theorem. Be clear!
Arrow's theorem asserts that no voting method based on rankings can satisfy the
four properties (or axioms) of nondictatorship, universal domain, Pareto
optimality, and independence from irrelevant alternatives. Since these four
properties are all desirable for a voting method, it simply states that an
ideal voting method does not exist!
Problem 2 (25 pts). An election is held between four candidates for
President of a booster club. The preference-ranking is as follows:
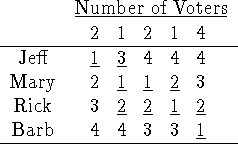
(a ranking underlined indicates that approval is given). Determine the
following (5 points each):
-
Who is the winner if the election is by plurality?
(Jeff 2 )
(Mary 3 )
(Rick 1 )
(Barb 4 )
Barb, with 4 votes, wins a plurality vote.
-
Who is the winner if the election is by plurality with run-off between the top
two candidates?
The next highest vote getter in plurality is Mary with 3, so she runs off
against Barb. Head to head, Mary gets 6 to Barb's 4. So Mary wins.
-
Who is the Borda winner?
(candidates traditional new )
(Jeff 17 33 )
(Mary 29 21 )
(Rick 29 21 )
(Barb 25 25 )
It's a tie between Rick and Mary.
-
Who is the winner by the approval method?
(Jeff 3 )
(Mary 4 )
(Rick 8 )
(Barb 4 )
Rick has the best approval score, so he wins.
-
Who is the Condorcet winner?
(Jeff 2 Mary 8 )
(Jeff 2 Rick 8 )
(Jeff 3 Barb 7 )
(Mary 5 Rick 5 )
(Mary 6 Barb 4 )
(Rick 6 Barb 4 )
Head-to-head results show that it's a tie between Rick and Mary, two weak
Condorcet winners.
Problem 3 (15 pts). Given the following preference-ranking (a ranking
underlined indicates that approval is given):
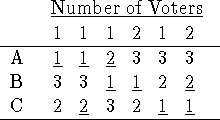
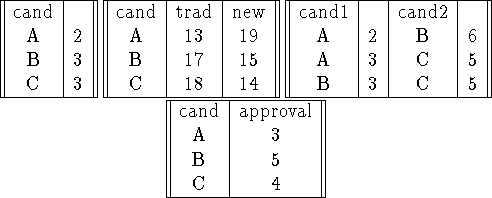
Table: Plurality, Borda, Head-to-Head, and Approval results
In the following assume that only the voters mentioned vote strategically in an
attempt to achieve a preferable outcome in the election specified. Will they succeed?
Explain!
-
The two voters who ranked B first and C second, in a Borda election.
Yes: if they rank C third, they'll remove two points from C (in traditional
calculation terms), and add two points to A. This will give B the win, with 17,
over C with 16 and A with 15.
-
The two voters who ranked C first and approved of two candidates, in an
approval election.
Yes: if they withhold their approval from B, then C will win with 4 over 3 for
the other two.
-
The voter who voted A second, in a plurality election with runoff between the
top two.
No: this voter already gave as little weight possible to C: in a runoff between
B and C, s/he can't increase B's vote count or reduce C's. If This voter votes
A first, then the runoff will be between A and C, and again C will win.
Problem 4 (10 pts). In a plurality election with 2000 voters, results are
in after 1000 votes have been counted:
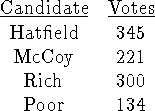
I (5pts): Poor is considering making his concession speech, and wonders how
many of the remaining votes he would need to get to be assured
of winning. As his campaign manager, tell him!
In the worst-case scenario, Poor would get x votes, and the other 1000-x
votes would go to the leader (Hatfield). Thus, for a tie, we'd have
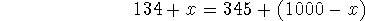
which gives
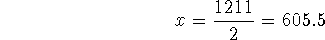
votes. For an assured win, then, Poor would need more than 605.5 votes, or 606 votes.
II (5pts): Faced with the prospect of part I, Poor wonders aloud ``What is the
smallest number of votes I could receive and conceivably win?''
Tell him!
In the best-case scenario, the others would tie, and Poor would get one or more
additional votes. In this election with 2000 votes and 4 candidates, an even
split gives each candidate 500 votes. Poor would need an additional vote to
win, so 501 votes. He'd thus need at least another 501-134=367 votes to win
under the very best of circumstances.
If Poor doesn't think this is possible, he may as well face the music and concede!
Problem 5 (15 pts).
I (10 pts). Is the following preference-ranking single-peaked with respect to
the order shown? (Show or explain.)
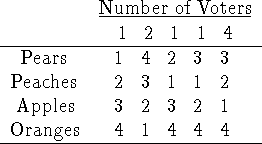
Yes, this ranking is single-peaked with respect to the order shown: to verify
this, plot the rankings against the order (1=pears, 2=peaches, 3=apples, and
4=oranges). Here they are (each letter represents the plot of one of the
rankings).
1 a b c d e
2 a b c d e
3 a b c d e
4 a b c d e
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
II (5 pts). Must a preference-ranking be single-peaked with respect to some
order to guarantee a Condorcet winner? (Explain!)
No! We saw examples in class in which every preference-ranking possible was
represented, and yet there was a Condorcet winner. Hence, single-peaked ranking
is not necessary for there to be a Condorcet winner, but it is sufficient for
there to be one.
Problem 6 (5 pts). In an election between 4 candidates with 12 voters,
the following Borda election results are reported:
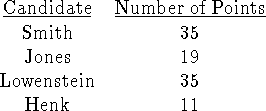
Is such a result possible? Why or why not? (``Yes'' or ``no'' answers will get
0 points: it's the reasoning that counts!)
Remark: the answer does not depend on which of the traditional or
``new/improved'' Borda point-calculation methods was used.
This result is not possible for at least two reasons:
-
Henk received only 11 points: each voter (of which there are twelve) must
assign him at least one point each, or 12 points.
-
The sum of the points allocated (100) is not equal to 12*10=120. Each voter
assigns 10 points, so something is wrong with this election!
Problem 7 (10 pts). Given the following preference-rankings for an
election to be held in your company (a ranking underlined indicates that
approval is given). You favor Bliss, but fear that Anger, Rudeness or Spite
might prevail. Choose an election strategy from among those discussed in class
(dictatorship not allowed!) to ensure that Bliss is the undisputed winner
(provided voters vote according to these preference-rankings).
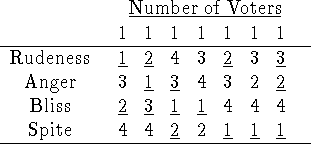
Bliss wins in a plurality election with run-off: Bliss and Spite receive 2 and
3 first-place votes, so meet head-to-head with Bliss winning 4 to 3.
Spite wins a Plurality and Borda election; there is no Condorcet winner; there
is a tie between Rudeness, Spite and Bliss for approval.
Problem 8 (10 pts). Do two of the following three parts, for 5 pts
each, and indicate clearly which two I am to grade (the third will not be graded!).
-
Explain why approval voting satisfies Pareto optimality.
If everyone approves of A over B, then A has at least as many approval votes as
B; hence B cannot win an approval election.
-
Give an example that shows how the approval method can violate the axiom of
independence from irrelevant alternatives.
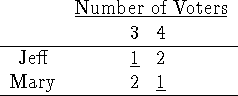
Mary wins. Now we introduce Candidate Barb:
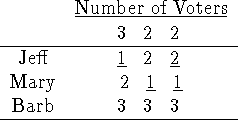
Jeff now wins.
-
An election is to be decided by the Condorcet method. In order to assure a
winner, the electors must choose from only single-peaked preference-rankings
with respect to a given order.
Why does this election violate the axiom of universal domain?
Since voters are not permitted to choose from among all preference-rankings
(but only those that are single-peaked), the axiom of universal domain is violated.


Next: About this document
LONG ANDREW E
Thu Sep 21 13:14:29 EDT 2000