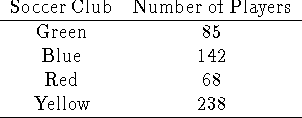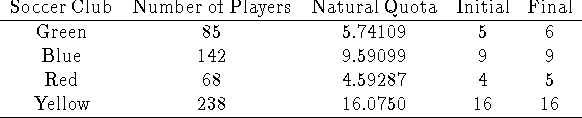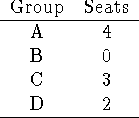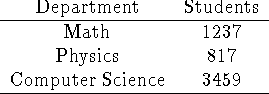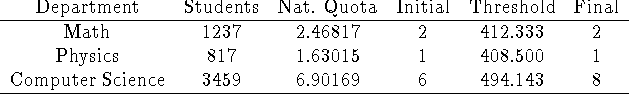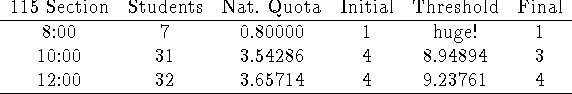

Next: About this document
Name:
Directions: Show your work! Answers without justification will
likely result in few points. Your written work also allows me the option of
giving you partial credit in the event of an incorrect final answer (but good
reasoning).
Indicate clearly your answer to each problem (e.g., put a box
around it).
Use three decimal places for natural divisor calculations.
Good luck!
Problem 1 (10 pts).
I (8 pts). Below are four terms or properties discussed in class and in this
chapter; following those are some possible definitions. Choose the most
appropriate definition for each term and place its letter in the box next to
the term.
-
 Quota Property
Quota Property -
 Population property
Population property -
 Alabama paradox
Alabama paradox -
 House Size property
House Size property
Possible definitions:
-
An example demonstrating the unfair allocation of seats for southern states in
the U.S. House of Representatives following the Civil War.
-
Given a fixed house size, no state whose population increases should lose a
seat to a state whose population decreases.
-
Given fixed populations, no state should lose a seat as the house size
increases.
-
A state's final allocation should not be one or more seats from its natural
quota.
-
An illustration of violation of the house size property.
-
Adding a new state with its fair share of seats can affect the number of seats
due other states.
II (2 pts). On what basis does the text assert that no ideal apportionment
method exists?
This is based on the fact that, while no quota property satisfies the
Population property, no divisor method satisfies the quota property: hence no
apportionment method studied (and the text asserts that no method in general)
can satisfy all the properties we consider essential for an ideal apportionment
method.
Problem 2 (40 pts).
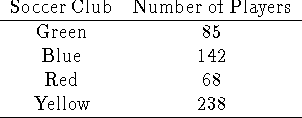
Distribute 36 soccer balls to these clubs according to the apportionments given
by the following methods:
-
Hamilton's method. We begin by finding the natural divisor, which is
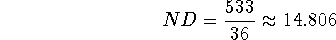
We're 2 under:
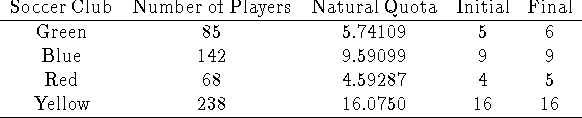
-
Lowndes' method - We're 2 under:

-
Jefferson's method - We're 2 under:

-
Webster's method - We're 1 over:

-
the Hill-Huntington method - We're 1 over:

Problem 3 (5 pts).
Given 4 groups, each with a population of over 100 people, and the need to
allocate 9 seats. You are told that, following an initial allocation of 7
seats using Lowndes' method, the final allocation is as follows:
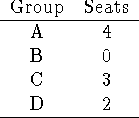
Is this allocation possible? Explain!
This allocation is not possible, because
Lowndes' method would give state B (with 0 seats) a seat after an initial
allocation left it empty-handed.
Problem 4 (10 pts).
Part I (5 pts).
Suppose that Webster's method allocates too many seats
upon initial allocation. Do we need to pick a smaller divisor or a larger one?
Explain!
If Webster's method allocates too many seats, then we need to pick a larger
divisor: smaller divisors correspond to larger house sizes, and vice
versa.
Part II (5 pts).
Explain the general strategy of divisor methods, including a description of the
significance of threshold divisors.
In general divisor methods work as follows: if the natural quota fails to
provide the correct house size, then
-
if the house size is too big, we need to find a smaller divisor;
-
if the house size is too big, we need to find a larger divisor.
There are many divisors that give the same house size. At certain threshold
values, the number of seats increases (or decreases) by one (or, in rare cases,
by more than one). Divisors that give the correct house size are found between
two threshold values.
In divisor methods, we seek these threshold values and then replace the
natural divisor by one of these appropriate divisors so as to assure the
correct house size.
The thresholds are dependent upon the method used: the thresholds for
Jefferson's method are different from Webster's, which are in turn different
from Hill-Huntington's method divisors.
Problem 5 (10 pts).
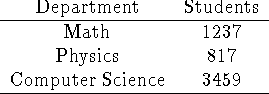
Using Jefferson's method, allocate 11 curriculum committee seats to the three
departments above based on their undergraduate student populations as given in
the table above.
The natural divisor is 501.182 (= 5513/11).
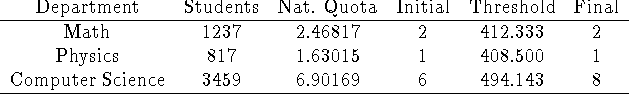
Initial allocation leaves us short by 2 seats. Computation of thresholds
suggests that we take 412.333, and hope that the quota property is holding. But
this gives a house size one too large, so we go back and compute the threshold
for CS to get its second seat:
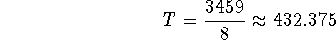
which means that before Math can get its third, CS will have taken two seats.
Problem 6 (10 pts). True/False: put T or F in the boxes at left.
-
 The Hamilton method satisfies the quota property. Basically by
definition!
The Hamilton method satisfies the quota property. Basically by
definition! -
 No apportionment method satisfies both the Quota property and the House Size
property. The book mentions the Quota Method of Balinski and Young as one
which does.
No apportionment method satisfies both the Quota property and the House Size
property. The book mentions the Quota Method of Balinski and Young as one
which does. -
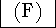 It is possible to exceed the house size in the initial allocation using
Jefferson's method. Because Jefferson's method uses truncation, it will
always initially produce a house size that is
It is possible to exceed the house size in the initial allocation using
Jefferson's method. Because Jefferson's method uses truncation, it will
always initially produce a house size that is 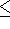 the desired house size.
the desired house size. -
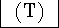 It is possible to exceed the house size in the initial allocation using
Webster's method. Because Webster's method uses rounding it can either
exceed or fall short of the desired house size.
It is possible to exceed the house size in the initial allocation using
Webster's method. Because Webster's method uses rounding it can either
exceed or fall short of the desired house size. -
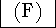 The cutoff for rounding between the two integers 7 and 8 using the
Hill-Huntington method is given by 7.5. Hill-Huntington uses the geometric
mean of the two numbers, or
The cutoff for rounding between the two integers 7 and 8 using the
Hill-Huntington method is given by 7.5. Hill-Huntington uses the geometric
mean of the two numbers, or 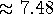
Problem 7 (10 pts).
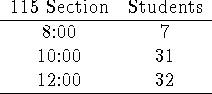
The enrollments for three sections of Math 115 are given above. The professors
decide to allocate 8 A grades among the students according to their
populations, using the Hill-Huntington method. Make those allocations!
Natural Divisor: 8.75
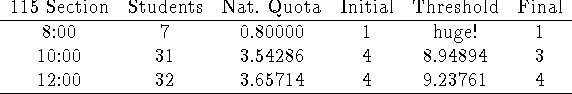
The 10:00 section gets fewer A grades allocated to it (its threshold is closer
to the natural divisor than the others). Just checking to see what folks would
do with the .80000 section.
Problem 8 (5 pts).
Apportion 12 seats to 3 states whose populations are given by the following
table using all five of the methods discussed in class (Hamilton's, Lowndes',
Jefferson's, Webster's, and Hill-Huntington's):

This works marvellously well: all methods, whether truncating or rounding,
assign the same number of seats in the initial allocation, which is precisely
the house size. How fortunate!


Next: About this document
LONG ANDREW E
Tue Oct 17 12:44:57 EDT 2000