Name:

Directions:

Show your work! Answers without justification will likely result in few points. That is especially important on this test, where an answer of `` '' without the reasoning behind it will not gain you full credit (and no credit if wrong!).

Indicate clearly your answer to each problem (e.g., put a box around your answer). Good luck!

Problem 1 (10 pts). Below are some terms or properties discussed in class and in this chapter; following those are several possible definitions. Choose the most appropriate definition for each term and place its letter in the box next to the term.

1. Law of large numbers
2. The basic counting rule
3. Permutation
4. Event
5. Universe

   Possible definitions:

   1. The set of all possible outcomes of an experiment.
   2. The probability of event or is the sum of the separate probabilities minus the probability of the event and .
   3. A subset of the set of all possible outcomes of an experiment.
   4. Gives the number of different ways of ordering n symbols, where the order makes a difference.
   5. Empirical probabilities tend to theoretical probabilities as an experiment is repeated over and again (as counts increase).
   6. If two tasks are to be carried out, with M ways of doing task 1 and N ways of doing task 2, then there are ways of doing them successively.

Problem 2 (4 pts). How is probability defined? (You should use the vocabulary of this chapter in making your definition.)

An experiment is conducted, and the number of possible outcomes enumerated (the Universe). A particular event E is the collection of outcomes satisfying some property, and the probability of event E is defined by

Problem 3 (10 pts). Consider the following experiment: a fair coin is tossed four times in succession. Use a single Venn diagram to represent the following:

1. The universe
2. The following two events:
   1. : An even number of heads
   2. : The first toss is tails
3. The intersection of the two events above (that is, event and ).

  
Figure 1: Problem 3

Problem 4 (5 pts). A farmer has five distinct fields. Each year each field must be plowed, planted and fertilized (in that order). In how many different ways can the farmer complete this sequence of tasks? (Assume that she works alone.)

We break this problem into tasks as follows: she

1. picks three slots for the first field,
2. picks three slots for the second field, etc.

Then there are choices for the first field, choices for the second field, etc. Final answer:

Wow! Talk about free choice!

Some students evidently thought that the question meant that the fields had to be completed once started, and hence thought that there were 5 tasks (do each field). In this case, there would be ways of attacking the work. No student explained this reasoning process, however. Talk to me! Tell me how you're proceeding, so that I may give you partial credit if you've got good ideas.

Problem 5 (10 pts). Two dice are rolled together.

1. What's the probability that the sum is 7?

   Here we can just do some counting, considering the 36 possibilities:

   

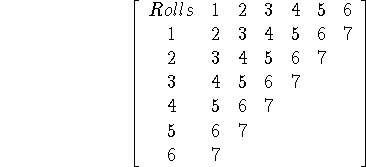
   The roll of die one is along the top, and the roll of die two is along the left side. In the table are the sums (those sums which are clearly above 7 have been suppressed). We see that 15 will result in a sum < 7, so

   

2. What's the probability that the product is 6?

   Similarly, consider the 36 possibilities:

   

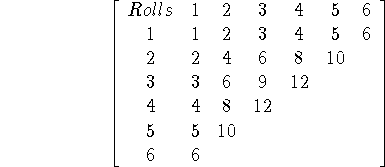
   In the table are the products (once again, those products which are clearly above 6 have been suppressed). We see that 10 will result in a product < 6, so

   

Problem 6 (10 pts). Suppose that 7% of a town's population have type A blood, 85% are Rh-positive, and 6% have type A blood and are Rh-positive.

1. What is the probability that a randomly selected individual in the town will have type A blood or be Rh-positive?

   Here we use the addition law, which says that

   

   so

   

2. What is the probability that a randomly selected individual in the town has neither type A nor Rh-positive blood?

   

Problem 7 (15 pts). A five card hand is drawn from a standard deck of 52 cards.

1. Give the following probabilities:
   1. That the cards are all of the same suit (``a flush'').

      First we'll count. We can break this into several tasks: find the number of

      1. hands possible (order doesn't count, repetition not permitted - combinations!):
      2. ways to choose the flush suit:
      3. ways to choose the five cards,
      Thus the probability is

      

   2. That no two cards are of the same value (that is, no pairs such as two queens or two tens are allowed).

      First we count. Find the number of

      1. ways to choose the five ranks of the cards:
      2. ways to choose one card from among four, (we have to do this for all five ranks).
      Thus the probability is

      

      Alternatively , you could do this using permutations (that is, assuming order counts) as follows:

      

      This would correspond to writing down slots and filling them. (There's alway more than one way!)

2. In how many ways can one obtain a hand containing exactly two pairs?

   Tasks:

   1. choose the two ranks from which to form the pairs:
   2. choose two cards from the first:
   3. choose two cards from the second:
   4. choose a card from the remaining 44:
   Total hands:

   

Problem 8 (5 pts). Fill in the following table with the appropriate counting technique.

 

Problem 9 (10 pts). A hand-recount of 1% of the ballots in the county of Palm Beach, Florida produces an additional 33 votes for Al Gore and 14 votes for George Bush in the Presidential election of 2000.

1. Based on this data, what is the empirical probability that an additional vote will go for Gore?

   The empirical probability p will be given by the ratio of new Gore votes (event of interest is a vote for Gore) to total new votes:

   

2. Assuming that this empirical probability accurately reflects the probability of finding missing votes for all of Palm Beach county, and that this 1% sample of the county was typical, how many votes will Gore pick up upon a hand-recount of the entire county? Give your answer rounded to the nearest integer.

   If Gore picks up 33 votes in each of the 100 sections of the county,

   

   votes.

Problem 10 (5 pts). Six hundred and thirty tickets are sold for a school raffle. If you buy 12 of them, what is the probability that you have the winning ticket? Give your answer as a decimal rounded to three decimals places.

Given that all tickets have the same probability, then the probability that you have the winning ticket is

Problem 11 (10 pts). In spite of your professor's wise advise, you foolishly engage in a Powerball lottery in which you choose 5 numbers from 1 to 49 (the white balls), and a red powerball with a number from 1 to 42.

1. How many different plays are there for the Powerball lottery (that is, how many distinct outcomes, or number choices, are possible)?

   In this case repetition is not permitted, and order doesn't count: hence the number of ways of completing the two tasks of choosing five white numbers and choosing one red number is the product

   

2. What is the probability of matching exactly one white ball, and the powerball?

   

Problem 12 (6 pts). Give an example in which each of the following counting techniques is applicable. (Do not give an example already mentioned in one of the problems on this exam, and explain how the counting method is appropriate for your example!)

1. 

   An example of this is when we study the order of birth of a couple's children, Boy/Girl, using B and G for the sex of the children. In this case, repetition is permitted and order is important (as first-born, last-born has traditionally been important in many cultures).

   Another example is a true/false exam, where T and F are used repeatedly (repetition permitted), and order is very important!

2. 

   These combinations are important when order is unimportant, but repetition is forbidden. Card hands and lottery picks are typical examples. Another example is the case of selecting people for a team (provided this is not a draft, in which order is important!). We want to know who's on the team, not the order in which they were named.

3. 

   Permutations are important when repetition is forbidden, and order is important. An example of this is a matching quiz: given 10 problems and 10 answers, match them up. The number of possible answers (assuming repetition is not permitted) is the number of permutations of 10 things taken 10 at a time. If there are more answers than questions (say 12 answers), then the number of possibilities is

• About this document ...