I also calculated the ratios of the errors, to see if I could discern a pattern in their change. Doubling the step-size cuts the error by a factor of 4 for trapezoid and midpoint; it cuts the error by a factor of 16 for Simpson's rule. This is as it should be, given the form of the error terms.
|
||||||||||||||||||||||||
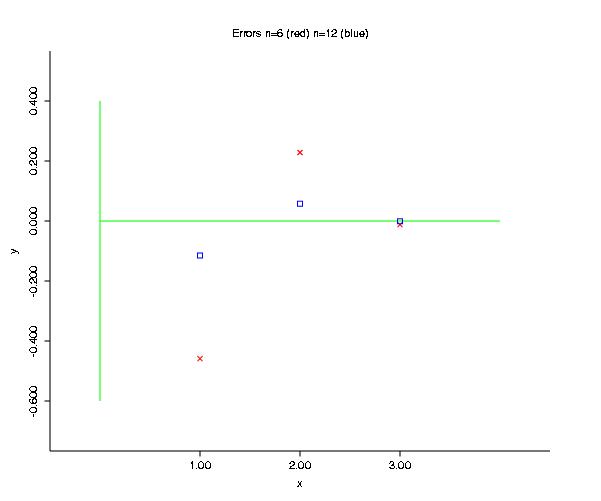
Here's a plot of the errors, for the two cases of n=6 and n=12. Trapezoidal errors are the greatest, then midpoint errors; you can see that if you double the midpoint error and add it to the trapezoidal error, the result should be about 0. This is the idea of Simpson's rule.

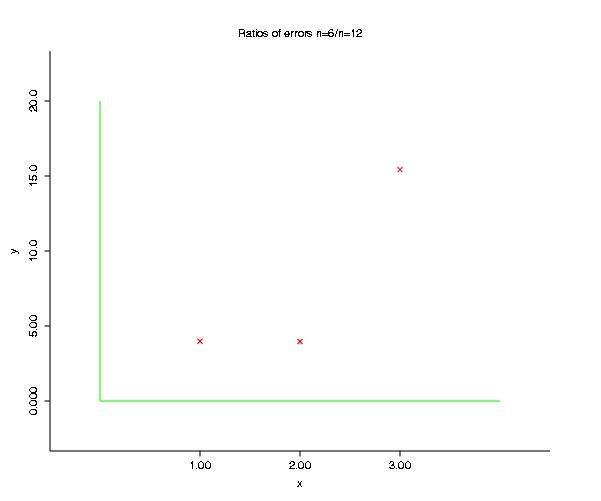
Just for fun, here's a plot of the ratios of n=6 errors divided by n=12 errors. You see that they're about a factor of 4 for a doubling of the number of steps n.
I used freely-available Xlispstat to generate these results (here's the xlispstat code I wrote to work this example). Ask me about it if you'd like to put xlispstat on your computer!