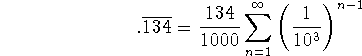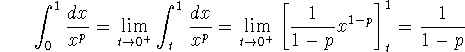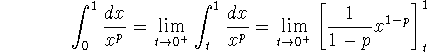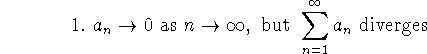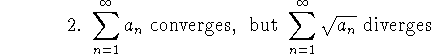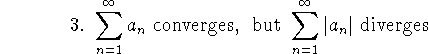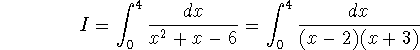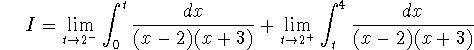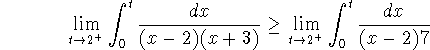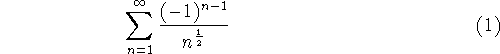

Next: About this document
Name:
Directions: Show your work! Answers without justification will
likely result in few points. Your written work also allows me the option of
giving you partial credit in the event of an incorrect final answer (but good
reasoning). Indicate clearly your answer to each problem (e.g., put a box
around it). Good luck!
Problem 1 (25 pts).
Determine whether the following sequences and series are convergent or
divergent (give valid reasons!). For those which are convergent find the
limit.
-

We can rewrite this as
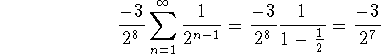
Convergent, by exhibition of the limit!
-

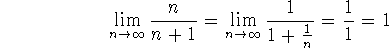
Convergent, as a monotone and bounded sequence converges to a limit.
-

For this infinite series to converge, we must have that the terms tend to zero
as 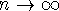 : i.e.,
: i.e.,

This is clearly not the case, as the argument to cosine would have to approach
multiples of 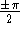 , and an integer argument of n will not do
so! Therefore, the series is divergent.
, and an integer argument of n will not do
so! Therefore, the series is divergent.
-
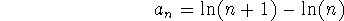
This simplifies to

and we can show that
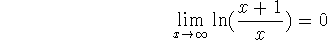
since 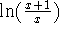 is a continuous function of its continuous argument
on this interval
is a continuous function of its continuous argument
on this interval 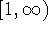 . Hence, the sequence is convergent with limit 0.
. Hence, the sequence is convergent with limit 0.
-
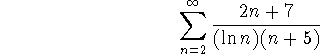
This is divergent, by comparison with

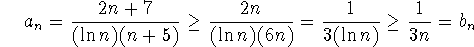
And since 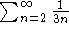 diverges, so does the given
series.
diverges, so does the given
series.
You could also proceed by the limit comparison test with 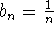 ,
and then show that
,
and then show that

diverges by comparison with the harmonic series, for example.
Problem 2 (5 pts). Express 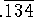 as an
infinite series.
as an
infinite series.
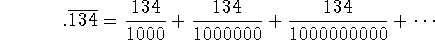
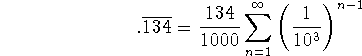
As a check, evaluate
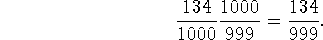
Problem 3 (10 pts). Analyze the integral

determining conditions on p for which it converges.
You should use the definition of the improper integral to do your
analysis (that is, use limits).
First of all, we note that if 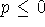 then the integral is perfectly well
behaved. Hence we consider in detail only the cases p>0.
then the integral is perfectly well
behaved. Hence we consider in detail only the cases p>0.
-
p=1 is special case:
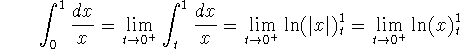
which diverges, since the limit does not exist as 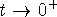 of
of 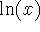 .
.
-
p<1:
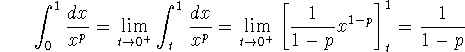
converges.
-
p>1:
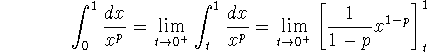
diverges, since the anti-derivative blows up as 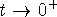 .
.
Thus, the answer is that for p<1 the integral is perfectly convergent;
otherwise it diverges.
Problem 4 (10 pts). Give examples of series for which
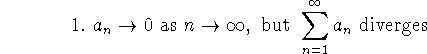
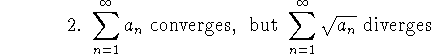
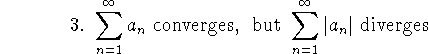

-

-

-

-

Problem 5 (10 pts).
-
State in precise terms (i.e., using
 ) what it means to say that
the sequence
) what it means to say that
the sequence 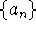 converges to the limit L.
converges to the limit L.
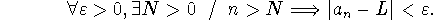
-
From your definition (and not using the algebra of limits) prove that
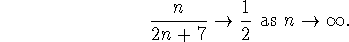
Given 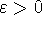 .
.
Consider
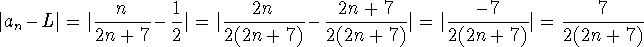
We now find where
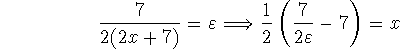
We take N to be the first positive integer greater than x. Then
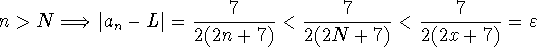
Q.E.D.
Problem 6 (10 pts). Decide whether the following integrals are
convergent or divergent (give reasons!):
-

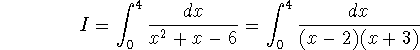
The problem occurs at x=2, where the integral is improper. I should be
written as the sum of two integrals,
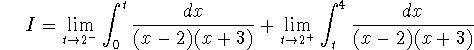
Neither one converges, as we can see by comparison, for example:
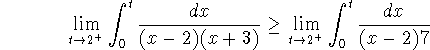
which, upon u-substitution, looks like

(and which fails to converge).
-

This converges by comparison:
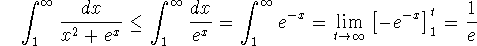
Problem 7 (5 pts). Find the values of p for which the series is
convergent:

Obviously if 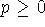 we're divergent, as the terms will grow at least
linearly. Hence consider p<0. We'll use the integral comparison
test. Consider
we're divergent, as the terms will grow at least
linearly. Hence consider p<0. We'll use the integral comparison
test. Consider

Now f is clearly positive on the interval 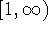 , but it needs to be
eventually decreasing if we're to use this test. Thus we consider the
derivative:
, but it needs to be
eventually decreasing if we're to use this test. Thus we consider the
derivative:
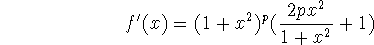
This must be negative for large values of x: that is, in the limit as 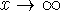 ,
, 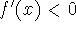 . Thus
. Thus
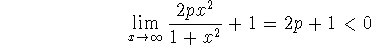
Thus, only in the event that 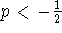 will this condition be satisfied. For
will this condition be satisfied. For
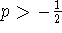 , f is increasing, which means the that series diverges (since the
limit of the terms cannot be zero). Thus, we can now restrict to
, f is increasing, which means the that series diverges (since the
limit of the terms cannot be zero). Thus, we can now restrict to 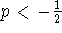 .
.
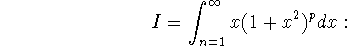
We use a u-substitution 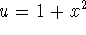 to write this as
to write this as

which converges if and only if p<-1. This then, is our answer: the series
converges if and only if p<-1.
Problem 8 (15 pts). Consider the series
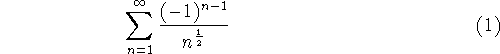
-
Demonstrate that the series converges, and use your calculator to estimate the
limit.
This converges by the alternating series test, as
-


and

-
The calculator will give rather strange results, however, as this series
converges slowly: I considered
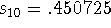 and
and 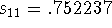 , and got
an average of .601481. The partial sum
, and got
an average of .601481. The partial sum 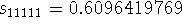 !
!
-
Plot the first 10 terms of the sequence
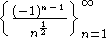 and the first 10 partial sums of the series (1) on the
same axes. Indicate clearly which graph is which.
and the first 10 partial sums of the series (1) on the
same axes. Indicate clearly which graph is which.
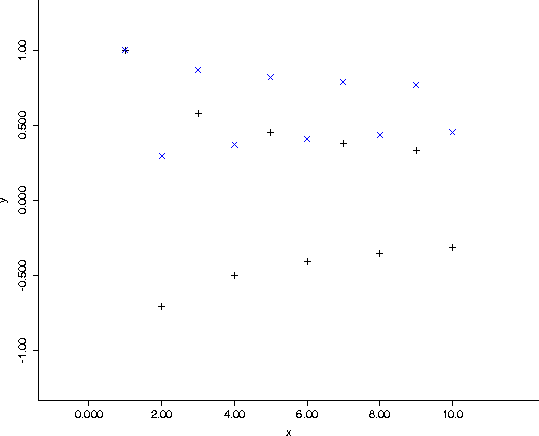
Figure 1: Problem 8: Terms in black, sums in blue.
-
How many terms m of the series (1) do we need to add in order to assure that
the size of the error incurred by approximating the series by the
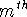 partial sum is less than .0001?
partial sum is less than .0001?
In order to assure that the error is less than .0001, we need to find m such
that
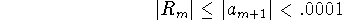
Hence we solve 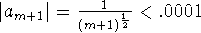 , or
, or

Thus, 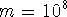 terms should work.
terms should work.
Problem 9 (10 pts). Consider the series

-
Use the sum of the first 20 terms to estimate the sum of the series.
1.2008678419584369
-
Bound the error of this estimate (that is, find values a and b
such that
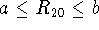 ``tightly'').
``tightly'').
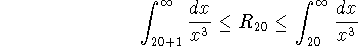
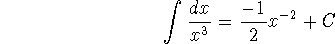
Hence
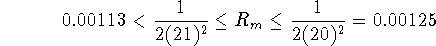
Problem  (Extra Credit: 5 pts). There are 2 million points in
the plane, no three of which are colinear. Is it possible to draw a line
through them so that exactly 1 million are on one side, and 1 million are on
the other?
(Extra Credit: 5 pts). There are 2 million points in
the plane, no three of which are colinear. Is it possible to draw a line
through them so that exactly 1 million are on one side, and 1 million are on
the other?

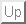

Next: About this document
LONG ANDREW E
Tue Nov 21 16:44:21 EST 2000

![]()
![]()

![]() : i.e.,
: i.e.,
![]()
![]() , and an integer argument of n will not do
so! Therefore, the series is divergent.
, and an integer argument of n will not do
so! Therefore, the series is divergent.
![]()
![]()
![]()
![]() is a continuous function of its continuous argument
on this interval
is a continuous function of its continuous argument
on this interval ![]() . Hence, the sequence is convergent with limit 0.
. Hence, the sequence is convergent with limit 0.
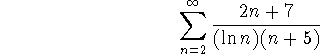
![]()
![]()
![]() diverges, so does the given
series.
diverges, so does the given
series.
![]() ,
and then show that
,
and then show that