MAT 220 001
Fall 2000
Test Two
1. (10 points)
Find parametric equations for the line through the point
(3,
-2, 1) and parallel to the line x = 1 + 2t, y = 2 t, z
= 3t.
2. (10 points)
Find an equation of the plane through the points (2, 4, 5),
(1,
5, 7), and (-1, 6, 8).
3. (10 points)
Find the point at which the line x
= 1 t, y = 3t, z = 1 + t intersects the plane 2x - y
+ 3z = 6.
4. (10 points)
Find the angle between the two planes 5x + y z = 10 and
x 2y + 3z = -1.
5. (10 points)
Find parametric equations of the line through (2, 3, 0) perpendicular to
and 
.
6. (15 points)
Find an equation of the plane that contains the intersecting lines x
= 3t 1, y = t + 1, z = t
1 and x = 5s 1, y = 2s + 1, z = -s
1.
7. (10 points)
Use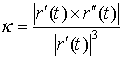 
to find the
curvature of the curve 
when 
.
8. (10 points)
Find parametric equations of the tangent line to the curve 
when 
.
9. (15 points)
A baseball pitcher throws a ball toward home plate 60 feet away. Assume that the pitchers mound is at the
origin and that home plate is on the positive x-axis at 
. We know that if the
pitcher can put a spin on the ball, the spin will cause a difference of air
pressure on the sides of the ball toward and away from the spin. This difference in air pressure causes a
spin acceleration. The acceleration of
the ball due to gravity and the spin is 
. The initial
velocity of the ball is 
. The pitcher throws
from the initial position 
.
9a. Find the velocity vector 
of the ball.
9b. Find the position vector 
of the ball.