- function - a rule which assigns a unique output to each input of the functions domain.
- domain - the collection of all possible arguments (or inputs) to a function.
- range - the collection of all values a function produces for the elements of the domain.
- The value of f at x is the result of feeding x to the function machine f.
- independent variable - a variable which represents the elements of the domain (usually plotted on the horizonal axis).
- dependent variable - a variable which represents the elements of the range (usually plotted on the vertical axis).
- graph - a set of ordered pairs of the form (x,y) or (x,f(x)), which we usually think of as a plot or visual representation of a function.
- piece-wise defined function - whose formula is different for different parts of its domain.
- absolute value function - a function which gives the distance of its argument from the origin; since its a distance, it's always positive!
- step-function - whose graphs go up or down like stair steps.
- even function - symmetric with respect to the vertical y-axis: f(-x)=f(x).
- odd function - symmetric with respect to the origin: f(-x)=-f(x).
- mathematical model
- scatter plot
-
increasing function:
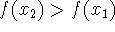 when
when 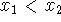 .
. -
decreasing function:
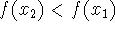 when
when 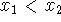 .
.
There are no explicit theorems in this chapter, although the vertical line test is really a sort of theorem: it tells us that a graph without multiple intersections with any vertical line represents a function (and that a graph with two intersections with a vertical line is not a function).
There are (at least) four representations of a function:
- verbal
- numeric (e.g. tables)
- visual (e.g. graph)
- algebraic (e.g. formula)
Convention: If a function is given by a formula and the domain is not stated explicitly, the convention is that the domain is the set of all numbers for which the formula makes sense. (thanks Tosin!
This section reviews the definition and properties of functions, and presents four ways to represent them (noted above). Properties studied include symmetry, monotonic behavior (increasing or decreasing), and the piece-wise definition of a functions. Some attention is paid to the vertical line test for whether a graph represents a function y=f(x), and to modeling real-life data with formulas.