- mathematical models - a mathematical description (e.g. formula or equation) and idealization of a real-world situation
- modeling process - a suggested method of performing math modeling (see p. 25)
- empirical model - a model created from data, rather than laws or principals
- interpolation - using a model to fill in between data points
- extrapolation - using a model to fill in beyond the data points
-
polynomial - a function made up of a weighted sum of integral powers of the
independent variable (usually x)
- coefficients - the weights for the powers of x in a polynomial
- degree - the highest power of x in a polynomial is its degree
-
Important types of polynomials:
- linear function - a polynomial of degree 1
- quadratic function - a polynomial of degree 2
- cubic function - a polynomial of degree 3
- rational function - a ratio of polynomial functions
- power function - a function which is a power of x (perhaps non-integral)
-
root function - a function of the form
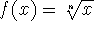where n is an
integer (this is equivalent to a power function of the form
) -
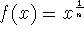exponential function - functions of the form
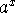
- logarithmic function - the inverse functions of exponential functions
- algebraic function - functions that are constructed using the basic operations (+, -, /, *, and taking roots) starting with polynomials.
- transcendental function - functions that are not algebraic.
There are no theorems in this section.
There are some handy rules of thumb for power functions, 
:
-
If a=n, where n is a positive integer:
- if n is even, then the graph looks like a flattened parabola
- if n is odd, then the graph looks like a flattened cubic
-
If a=1/n, where n is a positive integer:
- if n is even, then the graph looks like that of a flattened square root
- if n is odd, then the graph looks like that of a flattened cube root
Some properties of trigonometric functions are also discussed:
-
Periodicity: trigonometric functions are periodic: their graphs repeat
themselves. For example,
-
-
The functions
and 
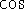are bounded by -1 and 1. That is, their values
are always found between -1 and 1. - ``In calculus the convention is that radian measure is always used (except when otherwise indicated).'' p. 33.
This chapter provides a summary of the variety of functions we encounter most often in this class, and shows how they can be used to model real world situations. The shapes of the graphs of these functions are seen repeatedly in a variety of data sets: hence, appreciation of and familiarity with the graphs of these functions can be important, as graphs of data can suggest mathematical models to us.