Section Summary: 2.5

1. Definitions
   • function continuous at x=a - a function f is continuous at a if

     

     The intuitive idea is that in a small neighborhood of x=a, the function f takes on values close to f(a). A function can be continuous from the left only,

     

     or from the right only:

     

   • function continuous on an interval - f is continuous on interval I if f is continuous at every point on the interval. An intuitive way of saying this is that the graph of f can be drawn without lifting pencil from paper.

   • function discontinuous at x=a - a function f which is not continuous at a. Types of discontinuities:
     • removable discontinuity - a hole exists in the graph because either f(a) doesn't exist, or is not the same as the limit

       

       (which must exist for the removable discontinuity).

     • infinite discontinuity - the function has a vertical asymptote at a

     • jump discontinuity -

       

       does not exist, because

       

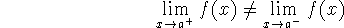
       There is a ``jump'' in the graph.

2. Theorems
   • If f and g are continuous at a, then
     • f+g
     • f-g
     • fg
     • cf for
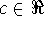
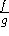     • (if )
     are all continuous at a.

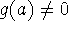     Here again, all the properties we'd like continuous functions to have are indeed satisfied: the sum of continuous functions is continuous, etc.

   • Polynomials, rational functions, root functions, and trigonometric functions are all continuous on their domains.

     This is one of the most important theorems in this section.

   • If f is continuous at b, and 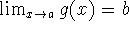, then

     

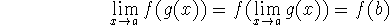
     Note that this is not the same as f(g(a)), which may not exist. Hence the composition is not necessarily continuous at a.

   • If g is continuous at a and f is continuous at g(a), then the composition 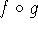given by

     

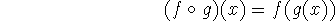
     is continuous at a, and

     

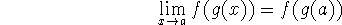
     ``A continuous function of a continuous function is continuous.''

   • Intermediate Value Theorem - Suppose that f is continuous on [a,b] and let N be any number between f(a) and f(b). Then there is a 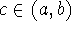such that

     

     (note: this only holds if ).

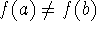     This theorem effectively says that in crossing a street you have to cross every line between the curbs and parallel to the curbs: you can't get from one side to the other without going through the middle.

3. Properties/Tricks/Hints/Etc.
   • The graph of a continuous function on an interval can be drawn without lifting the pen from the paper.

   • If f is continuous at a, then
     • f(a) is defined
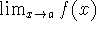     • exists, and
     • .

4. Summary

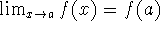   Continuity is defined and discussed in detail, along with varieties of discontinuities (jump, infinite, removable). Once again the theorems suggest that properties we'd like continuity to possess are true: e.g., the sum of two continuous functions is continuous; the composition of continuous functions is continuous. Entire classes of functions are continuous on their domains (polynomials, rational functions, trigonometric functions, root functions), so limits for these are easy to compute.

Problems:

Assignment: p. 112-114, #4-8, 13, 38, 40, 45, 48, 59

In class: #3, 10, 12, 16, 19, 33, 36, 44

• About this document ...