Make a list of all definitions in the section (a few words each is fine). Summarize any lengthy definitions introduced in this section in your own words.
-
A function y=f(x) may be defined implicitly by an equation
D(x,y)=E(x,y). Moving both functions to one side of the equation and defining
D(x,y)-E(x,y)=g(x,y), we see that this is equivalent to g(x,y)=0. That is,
rather than write y=f(x) explicitly, we write the relationship between
the two in another way. For example, the function
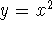can be written
explicitly, or as 
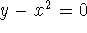. In the second case, it's not clear which is the
dependent and which the independent variable.
It's important to note that there may be multiple functions which are the solution of an implicit equation.
An example is the folium of Descartes, which is the solution(s) of the implicit equation
Here the equation is perfectly symmetric in x and y: it's not at all clear which variable is dependent, and which independent.
-
Implicit differentiation is the process of differentiating both sides of
an equation involving an independent variable x and dependent variable y by
x and solving the resulting expression for the derivative
. -
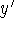Two curves are called orthogonal if at each point of intersection their
tangent lines are perpendicular; two families of curves are orthogonal
trajectories of each other if every curve in one family is orthogonal to
every member of the other.
Remember that two lines are perpendicular (or orthogonal) if their slopes
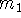and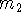 
satisfy the relationship 
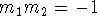(that is, their slopes are
negative reciprocals).
Make a list of all theorems (lemmas, corollaries) in the section (a few words each is fine). Summarize each one introduced in this section in your own words.
Didn't notice any.
Make a note of any especially useful properties, tricks, hints, or other materials.
I've caught our author in the act: in section 3.6 he says (p. 178) that ``...du/dx should not be thought of as an actual quotient.'' I said in class today that if it was good enough for Leibniz, it's good enough for me (i.e., that you can think of it as a quotient). Now in section 3.7 he says (p. 188) that ``The tangent line is vertical when the denominator in the expression for dy/dx is 0.'' Well, I say that if it's got a denominator, it's a quotient!
Summarize the section in two or three sentences.
Implicit equations are different than the explicit ones we have encountered most often to this point: we haven't ``solved'' for one of the variables in terms of the other (often we can not solve to find a unique function - there may be more than one, as in the solution of
- the equation of a circle of radius 1). The graph of the circle clearly fails the vertical line test, so this equation actually defines two different functions.
We can go ahead and differentiate both sides of the equation to get a new equation involving the derivative of the variable we'll treat as the dependent variable.
In this section we also look at orthogonal curves - those curves which have slopes at points of intersections which are negative reciprocals. These are introduced in this section because we're thinking about them as level curves of surfaces (e.g. the topographic maps, or weather maps in the exercises). An equation of the form g(x,y)=0 says ``where is the surface - i.e., the graph - generated by the function of two variables z=g(x,y) equal to 0?''