-
global (absolute) maximum at x=c:
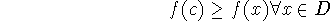
We will call f(c) the maximum value of f on Domain D.
-
global (absolute) minimum at x=c:
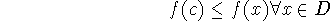
We will call f(c) the minimum value of f on Domain D.
- extreme values - maxima or minima
-
local maximum at x=c:
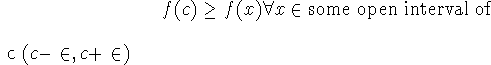
-
local minimum at x=c:
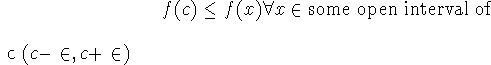
-
critical number of function f:
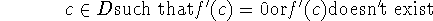
-
optimization problem - in which we seek the best way of doing something
(lowest cost purchase, greatest energy produced, etc.).
- Extreme Value Theorem: If f is continuous on a closed interval [a,b], then f attains a global maximum and global minimum on [a,b].
-
Fermat's Theorem: If f has a local max or min at c and
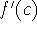 exists, then
exists, then 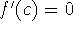 .
.
Rephrased: If f has a local max or min at c, then c is a critical number of f.
The closed interval method for finding global extrema:
- find f(c) for all critical numbers c;
- find f(a) and f(b);
- the largest of the lot is the global maximum, while the smallest of the lot is the global minimum.
We begin to use differentiation to help us to solve optimization problems. These problems are extremely common in business, government, and industry, as people are always trying to maximize or minimize something (e.g. energy expenditures, costs, number of hours worked, amount of labor required, transistors per chip, etc.)
While the derivative may help us to find extrema, we see that there are two potential problems with using the derivative alone: a function may not be differentiable at an extremum (e.g. there may be a corner in the graph, as in the function |x|), and the extrema may be found on the endpoints of a domain. These notions give rise to the definition of critical numbers, which are the elements of the domain which must be checked for extrema.