Section 1.2 Worksheet:

Assigned problems: Exercises pp. 35-37, #1, 2, 3 , 4, 6, 9, 13, 14, 16 (use regression line y = 4.8567x -220.967; no need to find it yourself). For exercises #3 and 4, use your calculator to plot the graphs as a check. (due Friday)

1. What is a mathematical model?

2. What are the four steps in the modeling process?

3. The most important model mathematicians use is the linear model,

   

   What is the graphical significance of m and b?

4. What is the objective of an investigator using linear regression? (This is a very common method used in many applications.)

5. Polynomials are fundamentally important: how do the terms degree and coefficient relate to polynomials?

6. Is a power function necessarily a polynomial? Sometimes a polynomial?

7. How does an empirical model differ from a theoretical model?

8. What are the periods of the functions 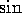, , and 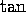? What identities tell us?

Notes:

1. Don't fret too much about algebraic versus transcendental functions.
2. Skim exponential and logarithmic functions. We'll come back to them in gory detail later.
3. Properties of trig functions are important!
4. In this class avoid root notation (e.g. 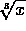); use power notation instead ( ).
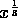5. Know the general shapes of the various functions.