Section 2.2 Worksheet:

Assigned problems: Exercises pp. 81-84, #4-16 even, 19, 30, 36 (due Thursday)

1. How do we read the expression

    

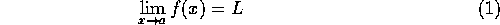
2. In expression (1) above, does x ever actually reach a?

3. How many ways can the limit

   

   fail to exist?

4. Examples 4 and 5 (p. 76) illustrate some pitfalls of guessing limits. What are they?

5. Come up with at least 5 qualitatively different ways in which the graph of a function can have a vertical asymptote.

6. What conclusion can we draw from example 2, p. 74?

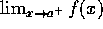7. If and 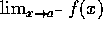exist, does 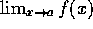exist?

Notes:

1. The function 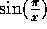, whose graph appears on page 76, is a truly bizarre animal. When you encounter strange functions like this, make a note of them!
2. Note the graph of 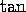(p. 81). Like the graphs of 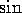and , you should be able to draw the graph of 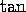in your sleep.