Name:

Directions: Show your work! Answers without justification will likely result in few points. Your written work also allows me the option of giving you partial credit in the event of an incorrect final answer (but good reasoning). Indicate clearly your answer to each problem (e.g., put a box around it). Good luck!

There are twelve 10 point problems. You may skip two - write ``skip'' on them. If you do not write ``skip'' on a problem, I will pick them at random to skip - so it's better that you choose!

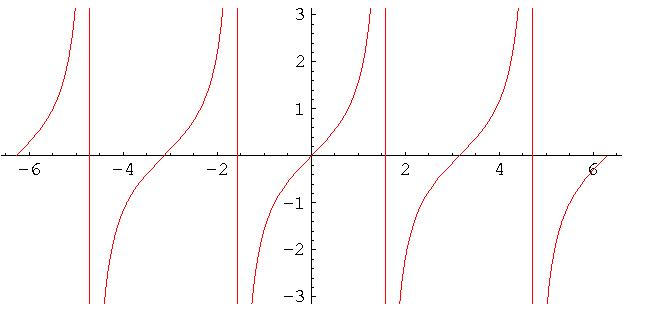
Problem 1 (10 pts). Given the graph of a portion of the tangent function,

1. Choose a suitable domain restriction, and draw the corresponding inverse function (arctan).
2. Describe properties of the arctan function that you can deduce from the tangent function (e.g. domain, range, symmetry, asymptotes, continuity, differentiability).

Problem 2 (10 pts). Consider the function

1. Is f invertible? If not, could you restrict the domain so that the restriction is invertible? In any event, explain your answer!
2. Write the formula for the inverse function of f or its restriction.

Problem 3 (10 pts). Hyperbolic trigonometric functions.

1. Define the and functions.
2. Derive the derivative of the inverse of the function using only the cancellation property of inverses (i.e. ) and the hyperbolic equation

   

Problem 4 (10 pts). Study the function

including details about the domain, range, symmetry, asymptotes, continuity, differentiability, max/mins, inflection points, etc. Use your calculator as needed.

Problem 5 (10 pts). Use L'H pital's rule (if appropriate) to compute the following limits:

1. 

2. 

3. 

Problem 6 (10 pts). Use the limit definition of the derivative to show that

Problem 7 (10 pts). Consider the region bounded by the function , the x-axis, and the line , and the solid obtained by rotating this region about the y axis. You are to set up the integral for the volume of the solid using two methods:

1. the method of cylindrical shells, and
2. the method of disks (washers - whatever!).

Use your calculator to compute the two integrals, and verify that they give the same answer. If they do not give the same answer, then indicate which you have the most confidence in!

Problem 8 (10 pts). If the work required to stretch a spring 1 ft beyond its natural length is 12 ft-lbs, how much work is needed to stretch it 9 inches beyond its natural length? (Draw a picture, write Hooke's law, and solve!)

Problem 9 (10 pts). Find the tangent line to the curve of the function

when t=1. Draw the curve and its tangent line at that point.

Problem 10 (10 pts). Use substitution to solve the following integrals:

1. 

2. 

Problem 11 (10 pts). True/false (feel free to explain any answer - you might get partial credit even if you're wrong!):

1. A function differentiable on an interval is necessarily continuous on the interval.
2. If a function has a slant asymptote as , then the function can be considered

   linear when x gets very large (positive).

3. 

   

4. If f is defined and strictly increasing on the set of all real numbers, and a<b,

   then f(a)<f(b).

5. The mean value theorem for integrals says that the average value of function f

   on the interval [a,b] is given by

   

Problem 12 (10 pts). A woman wants to design a rectangular garden with an ornamental fence on 3 sides which coses $3/foot. The back fence costs only $1/foot and she has only $200 to spend. What dimensions will allow a maximum area for the garden?