Test 5: Recent Concept Review

Section 6.2: volumes

• conceptualizing and drawing three-dimensional objects
• cross-sections of three dimensional objects (loaves of bread!)
• general volume method (when the solid is not of revolution):

  

  where A is the area of a cross-section.

• solids of revolution
• methods of disks and washers ( , or )

Section 6.3:

• method of cylindrical shells

  

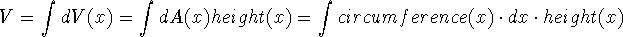
Section 6.4: Work

Work is the product of the force through its displacement:

When the force varies, or the distance varies, we need to do an integral. The two most common forms we saw were

• 

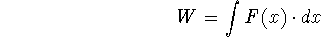
  and

• 

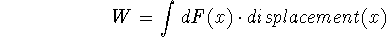
In the first case, a variable force F(x) operates through an infinitesimal displacement dx (e.g. for the work done by a spring over part of its motion); in the second, an infinitesimal force dF (e.g. a tiny chunk of weight, like a thin slice of water or cable) operates through a finite displacement (and both dF and d are functions of x).

Section 7.1:

• one-to-one functions (
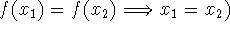
• demonstrating that a function is one-to-one (graphically using the horizontal line test; from the formula using the implication above)
• invertible functions
• graphing the inverse from the function by reflection about y=x
• properties of the inverse that derive from the function itself
• calculating the derivative of the inverse using implicit differentiation and the chain rule: since

  

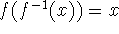
  by the chain rule,

  

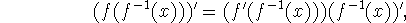
  so

  

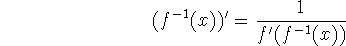
• poor notation (one could imagine that the inverse function 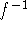means 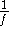; don't be deceived!)

Section 7.2:

• definition of exponential functions
• properties of graphs of exponential functions (base <1 and base >1).
• properties of exponential functions
• definition of e
• derivatives and integrals of exponential functions

Section 7.3:

• definition of logarithms
• properties of logarithms (``reflections'' of properties of exponentials)
• conversion of any logarithm of base a to base e

Section 7.4:

• derivatives of logarithmic functions
• logarithmic differentiation

Section 7.5:

• inverse trig functions, via domain restrictions
• domains, properties
• derivatives of inverse trig functions
• different ``branches'' of a function: when is 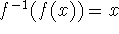, and when not?

Section 7.6:

• Definitions of hyperbolic trig functions
• derivatives, symmetry, inverses, and analogous properties to trig functions
• catenary, and where it appears in real life

Section 7.7:

• L'Hôpital's rule for indeterminate limits of the form 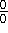and .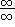
• Reexpressing other indeterminate limits in forms appropriate for L'Hôpital's rule
• Suppressing the urge to use L'Hôpital's rule for determinate limits!

Don't forget the basics from previous tests. While the focus will be on the new material, you will still be expected to be able to use the old!