Name:
Directions: Show your work! Answers without justification will
likely result in few points. Your written work also allows me the option of
giving you partial credit in the event of an incorrect final answer (but good
reasoning). Indicate clearly your answer to each problem (e.g., put a box
around it). Good luck!
Problem 1 (15 pts). For the function
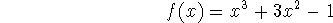
-
Use the first or second derivative test to determine where the function has
local maximum and local minimum values (indicate which).
-
Determine all intervals where the function is increasing.
-
Describe the concavity of the function.
Problem 2 (10 pts).
For the function
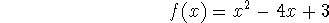
defined on the interval [-1,4], determine
-
the absolute maximum and absolute minimum values of f(x) over the
domain.
-
the value of x=c which satisfies the Mean Value Theorem.
Problem 3 (20 pts).
Cut square pieces from the corners of a  index card, and fold up
the sides to create a rectangular box. Determine the side length of the square
which determines the box with largest volume.
index card, and fold up
the sides to create a rectangular box. Determine the side length of the square
which determines the box with largest volume.
-
Draw a picture, using appropriate notation.
-
Write the volume equation in terms of a single variable.
-
Solve for the value of the side length which maximizes volume, and
calculate the volume.
-
Demonstrate that the extremum you found is, indeed, a maximum (rather than a
minimum).
Problem 4 (15 pts).
-
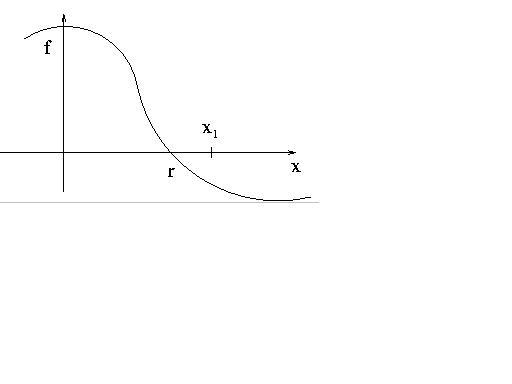
Carefully indicate the ``geometry'' of Newton's method by indicating the method
by which approximation
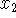 is derived from
is derived from 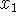 on the following
graph of function f. Determine the location of
on the following
graph of function f. Determine the location of 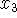 as well, based on your
drawing and the location of
as well, based on your
drawing and the location of 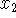 .
. -
Indicate a starting point on the graph of the function above for which Newton's
method would certainly fail to converge to the root r. Explain your
reasoning.
-
Given function
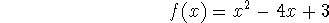
and initial guess 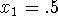 . How many iterations are needed to find a root to
within .001 of its correct value?
. How many iterations are needed to find a root to
within .001 of its correct value?
Problem 5 (15 pts). Given function

Use the information from the first and second derivatives to draw a careful
graph of the function, using your calculator as much as possible. In
particular, make sure you find all
-
maximum and minimum values;
-
inflection points and determine concavity;
-
asymptotes (including all vertical, horizontal, or slant asymptotes);
Draw the graph in all its glory, with intercepts, asymptotes, etc.!
Problem 6 (10 pts). True/False:
-
 If f has an absolute minimum value at c, then f'(c)=0.
If f has an absolute minimum value at c, then f'(c)=0. -
 The extreme value theorem assures us that a continuous function on the
open interval
The extreme value theorem assures us that a continuous function on the
open interval
(a,b) attains its absolute maximum and minimum values.
-
 If
If 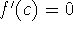 , then f has a local maximum or minimum at c.
, then f has a local maximum or minimum at c. -
 There exists a function f such that f(0)=2, f(2)=5, and f'(x)<1 for
There exists a function f such that f(0)=2, f(2)=5, and f'(x)<1 for 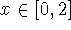 .
. -
 If f'(x) exists and is nonzero for all x, then
If f'(x) exists and is nonzero for all x, then 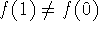 .
.
Problem 7 (15 pts). Sketch a graph which is consistent with the
following facts:
-
f is continuous and differentiable on its domain.
-
f(0)=4; f(-3)=0, f(2)=0.
-
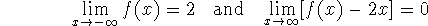
-
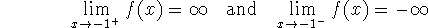
-
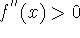 on (-1,3);
on (-1,3);
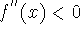 on
on 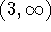 ;
;
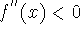 on
on 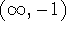 .
.
LONG ANDREW E
Wed Oct 24 11:46:58 EDT 2001
![]()
![]()
![]() index card, and fold up
the sides to create a rectangular box. Determine the side length of the square
which determines the box with largest volume.
index card, and fold up
the sides to create a rectangular box. Determine the side length of the square
which determines the box with largest volume.

![]()
![]() . How many iterations are needed to find a root to
within .001 of its correct value?
. How many iterations are needed to find a root to
within .001 of its correct value?
![]()
![]()
![]()