Problem Solutions

Section 2.5; pp. 112-113, #6 and 38

• #6: There are many functions that will satisfy this criterion: I'll graph two different ones

    
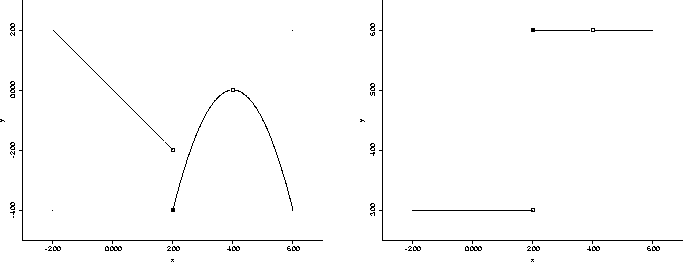
  Figure 1: Piece-wise defined functions for problem 6.
  

• #38: For this problem we have a piece-wise defined function

  

  We must find a value of c such that g is continuous on . Now g is clearly continuous on and since g is polynomial on each of these regions (quadratic on the first, and linear on the second). So the only remaining ``point of contention'' is the point x=4. The function is defined there, and continuous from the right:

  

  We need to make sure that the limit from the left is equal to this function value. Hence we seek c such that

  

  This is a quadratic equation, and we can solve it easily: it is equivalent to

  

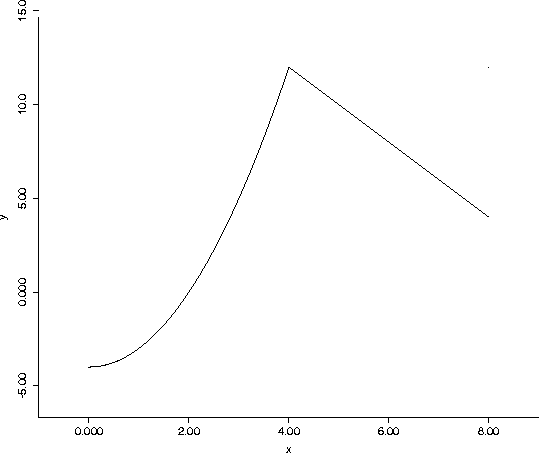
  So the solution is c=-2. Plugging this value of c into the function g, leads to the function given by the following graph:

    
  Figure: g with the value c=-2.
  

• About this document ...