Problem Solutions

Section 2.6; pp. 122-123, #3, 13

• #3: The graph looks something like this:

   

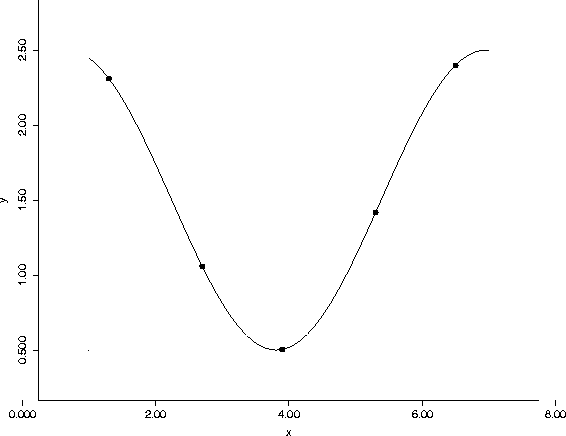
  The points, ordered from left to right, are labelled A through E. We are to list these five slopes in decreasing order, and explain our reasoning.

  The largest positive slope is clearly the fourth point from the right, D. Here the curve is the steepest. E follows closely behind.

  The slope at C is basically horizontal, or 0. The other two points have negative slopes, with the curve steepest (and hence most negative) at the second point, B.

  Thus, the decreasing ordering would be D, E, C, A, B.

• #13:
  1. Find the slope of the tangent to the curve

     

     at the point where x=a.

     We need to calculate the slope of the tangent line, using the limit process:

     

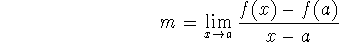
     which, in this case, give

     

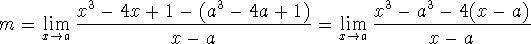
     As usual, we want to factor out a term of x-a from the numerator so that we can cancel it against the same term in the denominator:

     

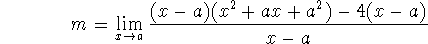
     We cancel and get a polynomial, which, being continuous, has an easy limit:

     

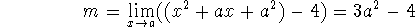
  2. So at the point (1,-2), the slope is 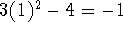so the equation of the tangent line is given by

     

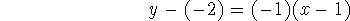
     or

     

     At the point (2,1), the slope is 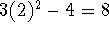so the equation of the tangent line is given by

     

  3. A graph and some tangent lines:

       
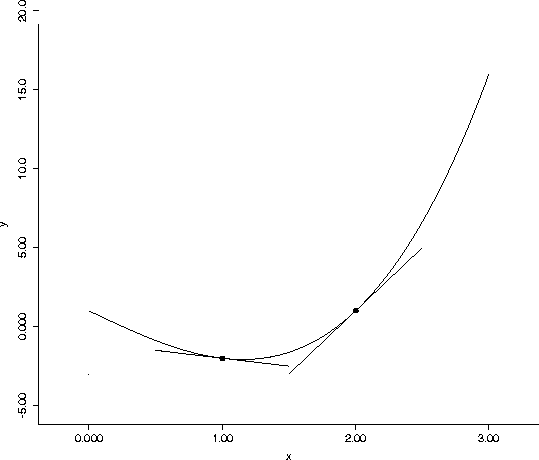
     Figure: The graph of g and its two tangent lines at the points x=1 and x=2.
     

• About this document ...