Make a list of all definitions in the section (a few words each is fine). Summarize any lengthy definitions introduced in this section in your own words.
-
derivative of a function f - denoted by
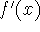 ,
,
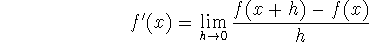
Synonyms for the derivative function:
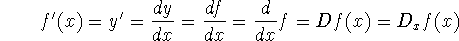
This function simply associates with each element a of the domain the slope of the curve (i.e. the slope of the tangent line) at the points x=a
-
differentiation operators - The symbols D and d/dx in the synonym
tree above are called operators: they operate on the function f to produce a
new function (the derivative function)
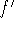 .
.
The difference between operators and functions is one of domain: an operator takes as its domain something more general than numbers. In this case, these operators take functions and return functions; their domains are sets of functions, and their ranges are functions. Thus we might write

whereas an ordinary function, like
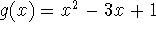 , would be written
, would be written
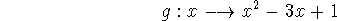
-
differentiation - The operation referred to above: the operation of
creating the derivative function
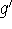 from a given function f.
from a given function f. -

This produces some synonyms for the derivative at x=a,
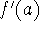 :
:
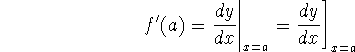
We think of all of these as being evaluated at a.
-
differentiable -
A function f is differentiable at a if the derivative
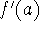 exists. It is differentiable on an open interval (a,b) [or
exists. It is differentiable on an open interval (a,b) [or
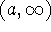 or
or 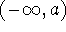 or
or 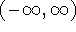 ] if it is differentiable at
every number in the interval.
] if it is differentiable at
every number in the interval.
We might think of differentiability implying the ability to get a derivative at a point; it implies the existence of a derivative.
- vertical tangent line - a place where the tangent line to the curve is vertical. The slope in this case is infinite, so the derivative doesn't exist at points with vertical tangent lines.
Make a list of all theorems (lemmas, corollaries) in the section (a few words each is fine). Summarize each one introduced in this section in your own words.
If f is differentiable at a, then f is continuous at a.
For the derivative to exist, the function must be defined at a (so f(a) exists), then the limit of f(x) must exist and approach the value f(a) at a. This is the essence of continuity, however: hence, differentiability implies continuity.
Note: it is not true that if f is continuous at a, then f is differentiable at a. For example, continuous function with a corner at x=a is not differentiable there.
Make a note of any especially useful properties, tricks, hints, or other materials.
-
Figure 3, p. 138 is terrible! (Figure 2 is the one to focus on - it looks
good). We might, however, use this to show the problems of estimating
derivatives from table data. Notice that the function I(t) is shown as
constant from 1985 to 1987 (the graph is flat over this interval). This means
that the derivative at each point between those years should be 0. But
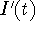 is shown as positive over that time. Ouch! Don't pay attention to
that, except perhaps to find other irregulaties in the graphs.
is shown as positive over that time. Ouch! Don't pay attention to
that, except perhaps to find other irregulaties in the graphs. -
Ways in which a function can fail to be differentiable at a:
- discontinuities of all sorts
- corners in continuous functions
-
continuous functions at places with vertical tangent lines: the slope
of such lines is either
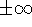 , but the derivative must be
finite.
, but the derivative must be
finite.
Summarize the section in two or three sentences.
In this case we take the derivative as defined in section 3.1 one step further:
if for each value of a there is something called ![]() , then we could
write
, then we could
write
![]()
which means that with every value a of the domain, there is associated a
value ![]() of the range. Hence we can think of
of the range. Hence we can think of ![]() as a
function (the slope function, which gives the slope of the curve at any point
of the graph - where defined).
as a
function (the slope function, which gives the slope of the curve at any point
of the graph - where defined).
The slope might not be defined for a number of reasons: the graph may be discontinuous (have a hole, or jump, or infinite discontinuity); the graph of a continuous function may have a corner (where the tangent line is not defined); or a smooth, continuous function may have a tangent line with infinite slope.
Note that in the definition of the derivative function we simply replace the value of a with x: we've been thinking of a as a fixed number, but now that we want to think of a as varying, we replace it with x (to make you think of it as a variable).