Make a list of all definitions in the section (a few words each is fine). Summarize any lengthy definitions introduced in this section in your own words.
Didn't notice any!
Make a list of all theorems (lemmas, corollaries) in the section (a few words each is fine). Summarize each one introduced in this section in your own words.
For the following, we assume that f and g are differentiable functions.
-
The slope of the line y=x is 1:
-
-
where n is an integer. This rule is very useful, since polynomials include so many terms of this form.
-
Multiplying a function by a constant scales it in the y direction. This makes
it steeper by a factor of c:
-
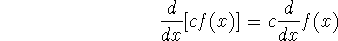
``The derivative of a sum is the sum of the derivatives.''
-
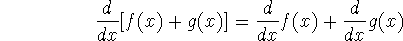
``The derivative of a difference is the difference of the derivatives.''
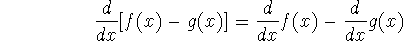
The product rule may seem a little counter-intuitive; it certainly isn't as simple as a product of derivatives (however much we'd hope so):
-
-
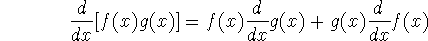
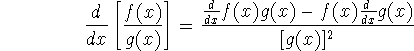
I just recently learned a rhyme to remember this formula:
``Lo dee hi minus hi dee lo, over the denominator square we go!''
It's sometimes represented this way:
-
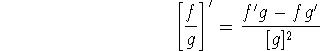
The power rule generalizes to this:
where
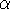is a real number. An important special case is the following:
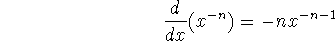
where n is an integer.
A constant function is flat, horizontal; its slope is 0:
Make a note of any especially useful properties, tricks, hints, or other materials.
``The theorems of this section show that any polynomial is differentiable on
and any rational function is differentiable on its domain.''
Examples:
- Example 3: combines rules to show how to differentiate general polynomials.
- Example 4: reminds us that points where the derivative is 0 are places where the tangent line is horizontal.
- Example 5: demonstrates the product rule.
- Example 6: Even though we don't know the form of g, we have enough information about it to answer the question posed.
- Example 7: demonstrates the quotient rule with a rational function.
- Example 8, 9: demonstrate that the power rule is not just for positive integers anymore!
- Example 10: reminds us that finding the tangent line to a curve at a given point reduces to finding the slope at that point, which is a derivative issue. Then we can use the point-slope form.
-
Example 11: If we're asked to find where the tangent line is parallel to
a second line, then we are to find places where their slopes are equal. Find
the slope of the target line, and set the derivative (i.e. the slope of the
tangent) equal to that value.
Summarize the section in two or three sentences.
This section is replete with formulas for some of the most important functions we will be working with (these formulas must be committed to memory!). It began with a few special cases, then began extending to general cases: several of these follow our intuition, e.g. the sum rule (the derivative of a sum is the sum of the derivatives); others are not so intuitive (the product and quotient rules are not obvious). There were many examples which demonstrated how one uses these formulas.
Proofs are given for these special formulas, and, for the most part, are not too complicated. One proceeds directly from the definition of the derivative function as the limit
and one hopes that things just fall out!