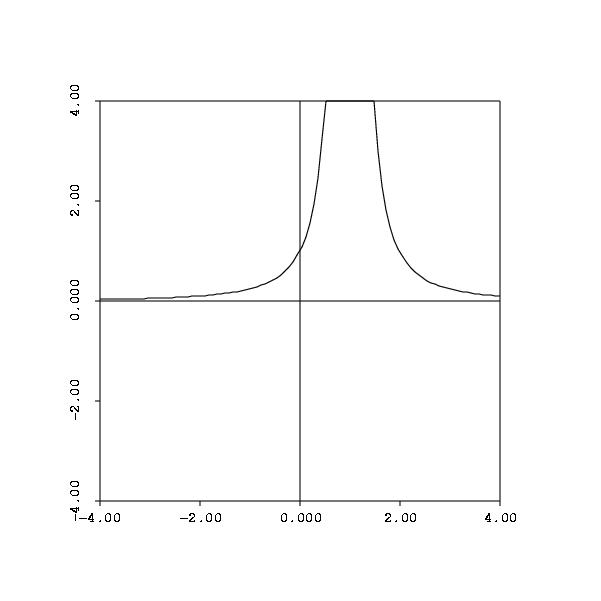
f(0)=f(2)=1. The problem, of course, is that the function is undefined at x=1, so the mean value theorem doesn't apply.
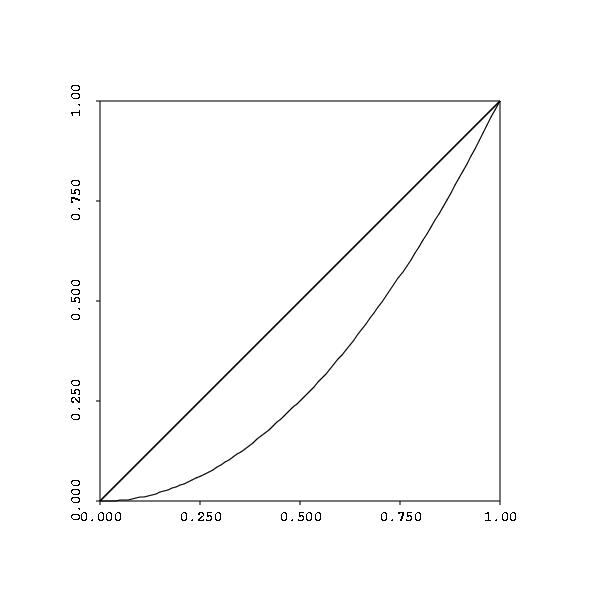
The graph above represents the case where the two runners start at the same point, then arrive at the same point at one unit of time later (t=1). If we consider the difference of the two functions, then we have that f(0)=f(1)=0. If we impose the condition that the function f be continuous, then the hypotheses of Rolle's theorem are satisfied, and we can conclude that there exists a c in the interval [0,1] where f'(c)=0, which means that g'(c)=h'(c), or that the velocities of the two runners are the same at c.
Website maintained by Andy Long. Comments appreciated.