Make a list of all definitions in the section (a few words each is fine). Summarize any lengthy definitions introduced in this section in your own words.
None that I saw.
Make a list of all theorems (lemmas, corollaries) in the section (a few words each is fine). Summarize each one introduced in this section in your own words.
-
Rolle's Theorem: Let f be a function that satisfies the following
three hypotheses:
- f is continuous on the closed interval [a,b].
- f is differentiable on the open interval (a,b).
- f(a)=f(b)
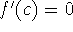 .
.
Rolle's theorem says that if a function sets off continuously and smoothly (differentiably) from one y-value and returns to that same value later on, then there was a moment when the function turned around. When it did, its value of dy/dx was zero (i.e., there was a c such that
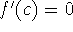 ).
). -
The Mean Value Theorem:
Let f be a function that satisfies the following
hypotheses:
- f is continuous on the closed interval [a,b].
- f is differentiable on the open interval (a,b).
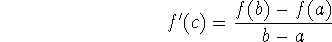
or, equivalently,
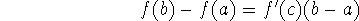
You can think of the mean value theorem as Rolle's theorem, just tilted! And that's how it is proved: by ``tilting'' a function so that we can apply Rolle's theorem.
-
Theorem: If
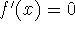 for all x in an interval (a,b), then f is
constant on (a,b).
for all x in an interval (a,b), then f is
constant on (a,b).
Corollary: If
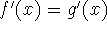 for all x in an interval (a,b),
then f-g is constant on (a,b); that is, f(x)=g(x)+c where c is a
constant.
for all x in an interval (a,b),
then f-g is constant on (a,b); that is, f(x)=g(x)+c where c is a
constant.
The theorem is proven by the Mean Value Theorem; the corollary by application of the theorem.
Make a note of any especially useful properties, tricks, hints, or other materials.
``The main significance of the Mean Value Theorem is that it enables us to obtain information about a function from information about its derivative.''
Summarize the section in two or three sentences.
This section presents a few theorems (notably Rolle's theorem, and the Mean Value Theorem) which will prove useful in certain types of problems. For example, if a position function is defined on a time interval, the average speed of the particle must match up with an instantaneous speed at some point in time.
The proof of Rolle's Theorem is nice, as it relies on nothing more than the Extreme Value Theorem, and Fermat's Theorem, which were presented in the previous section. This is how theorems are often used: to prove other theorems!