Make a list of all definitions in the section (a few words each is fine). Summarize any lengthy definitions introduced in this section in your own words.
- concave upward on interval I: the graph of f lies above all of its tangents on the interval I.
- concave downward on interval I: the graph of f lies below all of its tangents on the interval I.
-
inflection point: Point P on a curve is an inflection point if the
curve changes concavity at P.
``There is a point of inflection at any point where the second derivative changes sign.'' (p. 244)
Make a list of all theorems (lemmas, corollaries) in the section (a few words each is fine). Summarize each one introduced in this section in your own words.
-
Increasing/Decreasing Test:
If
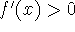on [a,b], then f
increases on [a,b];
if
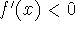on [a,b], then f
decreases on [a,b]. -
The first derivative test: Let c be a critical number of f.
If
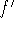changes sign from positive to negative at c, then f has a
local maximum at c.
If
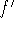changes sign from negative to positive at c, then f has a
local minimum at c.
If
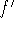does not change sign at c, then f has neither a max nor a min
at c. -
Concavity test:
If
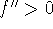for all x in interval I, then f is
concave up on I;
if
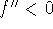for all x in interval I, then f is
concave down on I.
Just remember the two types of parabolas: bowls and umbrellas. Bowl:
,
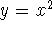so 
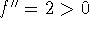, and the curve is concave up; umbrella: 
,
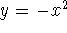so 
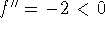, and the curve is concave down. -
Second derivative test: Suppose
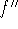is continuous near
c.
If
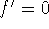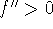and , then f has a local
minimum at c;
If
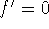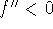and , then f has a local
maximum at c.
The second derivative test is inconclusive if
.
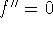Make a note of any especially useful properties, tricks, hints, or other materials.
You'll notice that there are some nice tables which are created to show the sign of the derivative and hence indicate the direction (increasing/decreasing) of the function's graph; this is a graphing aid.
Summarize the section in two or three sentences.
Knowledge of and inform us about critical aspects
of f (increasing/decreasing, extrema, points of inflection, concavity).