Let's look at three different approaches to computing the integral
You might notice first of all that the integrand is a difference; and we know that the integral of a difference is the difference of the integrals, so that
Now the integral 
is easy, but 
might cause some consternation.
If you know an antiderivative of |x-1|, then you might proceed directly to
compute the integral. But you might also proceed by using the definition of the
absolute value function to work this problem:
Now we can divide the interval of integration, [0,2], up into two intervals, so that
and we replace the expression |x-1| with the appropriate form from the definition:
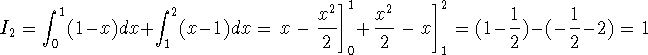
The first part of the integral I is easy:
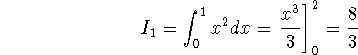
Hence, 
.
Now for the first ``improvement'': let's use symmetry. |x-1| is even on the interval [0,2] (as we see at left below):
we could compute as follows:
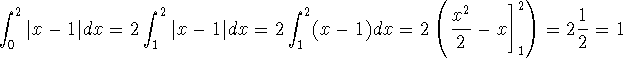
Alternatively, as mentioned, we could compute the integral directly if
only we know an antiderivative. Now, to compute the antiderivative, we can
return to the piecewise formula, and integrate each term:
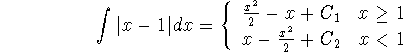
Integration is a smoothing operation, so the antiderivative of a continuous but non-differentiable function (e.g. |x-1|) is differentiable - smoother than its derivative. We need to arrange for the constants in the formula of this antiderivative in such a way that it is continuous. Thus we evaluate both formulas of the piecewise function at x=1 so that
So we conclude that 
, or 
, and we can write
the general antiderivative as
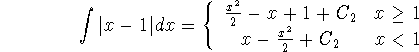
and choose 
to make life easy (see the figure at right above):
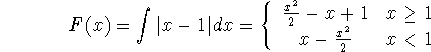
Then
