Section Summary 6.5: Average Value of a Function

1. Definitions
   • average value of f on the interval [a,b]:

     

2. Theorems
   • Mean Value Theorem for Integrals: If f is continuous on [a,b], then there exists a number c in [a,b] such that

     

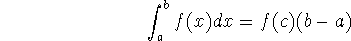
     Proof (Problem 21, p. 401): Prove the Mean Value Theorem for Integrals by applying the Mean Value Theorem for derivatives (see Section 4.2) to the function .

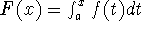     The mean value theorem says that, for continuously differentiable F on interval [a,b], there exists 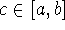such that

     

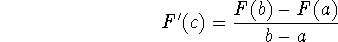
     Now in this special case with 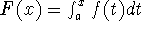, the fundamental theorem of calculus tells us that F'(x)=f(x), so

     

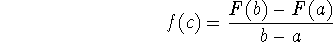
     Furthermore, by definition of F and using one property of integrals,

     

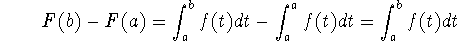
     so we can conclude that

     

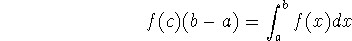
     which is what we needed to prove. QED.

3. Summary

   In this section we discover how to compute the average of an infinite number of values (along an interval), using a version of the mean value theorem for integrals.

   One way of thinking about this is as an area problem, especially in the case where on [a,b]: the integral of f over [a,b] represents an area A. We want to find a rectangle on the same interval with the same area as A. Clearly a rectangle whose height is the maximum of f would be too much, in general: it would contain all the area A and then some; a rectangle whose height is the minimum of f would be too little, since portions of A would be outside this rectangle. Somewhere between the two heights we have the equal area rectangle. Since f is continuous, the height would be equal to the value of the function at some intermediate value f(c) at .

Problems:

Problems, pp. 400-401, #1, 4, 12, 15, 16, 18, 20

At the board: #3, 11, 15

• About this document ...