Section Summary: 7.7 - L'Hôpital's rule

1. Definitions

2. Theorems

   • L'Hôpital's rule: Suppose f and g are differentiable and 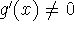near a (except possibly at a). Suppose that

     

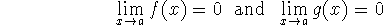
     or that

     

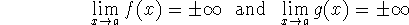
     Then

     

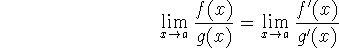
     If the limit on the right side exists (or is 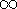or ).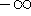

     These quotients are called indeterminate forms, since we can't tell which way they'll turn out by inspection.

3. Properties/Tricks/Hints/Etc.
   • Other indeterminate forms include products 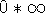, which we can rewrite as quotients: e.g.

     

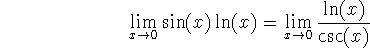
   • Differences can be indeterminate, e.g. 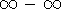, which we may also be able to rewrite as quotients: e.g.

     

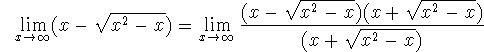
     so

     

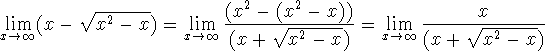
     which we see is an indeterminate form as a quotient.

   • If

     

     is indeterminate, then you can apply the rule again (provided the derivative functions satisfy the constraints of the theorem):

     

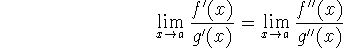
     etc. This could go on for a long time!

4. Summary

   There are certain limits that are indeterminate, and L'Hôpital's rule provides us a method for determining them! There are a few more forms that are indeterminate (e.g. powers), but we just don't have enough time to worry about them as the semester winds down - so don't worry about them!

Problems:

Problems, pp. 493-495, #16, 17, 25, 28, 43, 54, 72

On the board: 9, 21, 27, 41, 52

• About this document ...