Day 19 in math modeling

• Hand in exercises and Project 3.2 from Chapter 3
• Exercise #7, p. 226

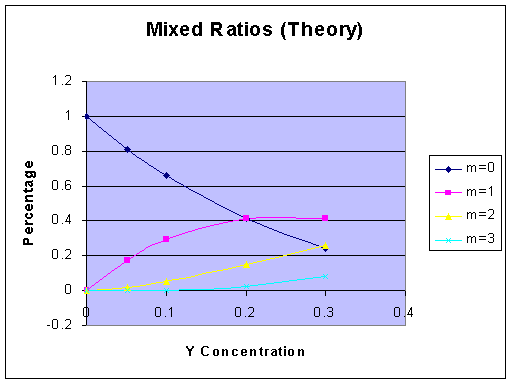
8. Examples (continued):
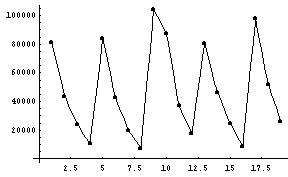
   • Lynx data:
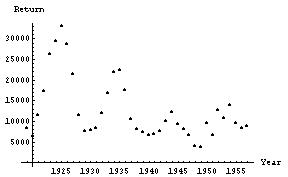
     • Long term trend: horizontal asymptote (perhaps zero!)
     • Decaying oscillations (some periodicity)
     • Book's modeling process:
       1. Capture decreasing trend with linear model (linear regression: y=mt+b)
       2. "Detrend" the data, creating new variable z_i = y_i - (mt_i+b)
       3. Guess period of oscillations of z
       4. Determine amplitude "envelope" of the damping (using linear regression on ln(abs(z)) for the peak data, to estimate exponential model f(t)=exp(Mt+B))
       5. Put it all together: estimate the model
          y(t)=a + b*t + c*f(t)sin(2 pi t / 10) + d*f(t)sin(2 pi t / 10)
       Violates horizontal asymptote assumption....

     Notes:

     • this model is linear in the parameters a, b, c, and d.
     • ultimate behavior of model: leads to negative numbers of lynx

   • Corn Storage example (more later: section 4.13). Correlation: -0.02
     

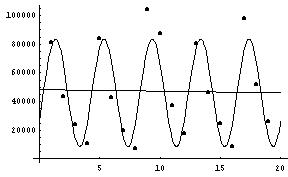
   • Bear data - intrinsically non-linearizable model: the logistic
     • 
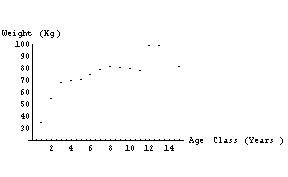
       • long term trend: horizontal asymptote
       • concave down? Increasing with decreasing slope....
       • positive y-intercept
       • model: logistic
         y(t)=K/(1 + Cexp(-rt))
         or y(t)=K/(1 + exp(-r(t-t₀)))

     • "With nonlinear problems such as the logistic, choosing good [initial parameter] guesses is essential." (p. 183)

   • Jack's Project: a nonlinear regression problem
     
     

9. Interpolation
   • Interpolating n+1 points with an n^th degree polynomial - a bad idea? ("saturated model")

   • An easy example(?) from Mensa and my cereal box:

     4	6	4	8
     5	2	9	3
     1	2	3	1
     5	5	8	?

     The text reads: "Following the same logic used for the first 3 triangles, fill in the missing number on the fourth triangle." (my emphasis)

     This illustrates the pervasiveness of "linear reasoning". Mathematicians can find infinitely many functions that will "fit" this data - exactly! (An exact fit to data is the very definition of interpolation.) "Mensa" has fixated on the linear solution, which is typical but unfortunate, especially for a society of "geniuses". How can we follow "the same logic" when an infinite number of logics give different answers?

     Now - for the $25,000 question, and a chance to get into Mensa - what is the Mensa answer?

   • Spline: a function built piecewise out of curve segments, with some smoothness condition
     • linear spline - use straight line segments (continuity)
       

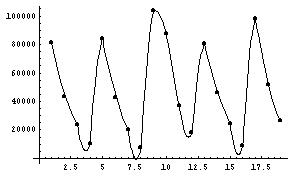
     • quadratic spline - use parabolas (differentiable)
       

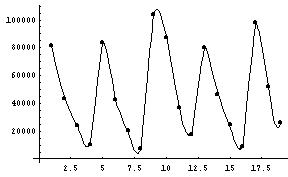
     • cubic spline - use cubics (twice differentiable)
       

   • Exercise #7, p. 226: How-to, why-to.

   • Interpolating noisy data
     • "[T]he human eye can be as good at curve fitting as any algorithm." p. 195.
     • That said, here's the human eye algorithm:
       • plot data carefully
       • draw (by hand) the perceived trend
       • pick reference points
       • interpolate reference points

Note:

• Mathematica file to generate the Corn Storage figures and models, etc.