The problem is to estimate the number of dots in the square. We are told that we should not attempt to count "a large number of dots", but that counting a sample is appropriate.
The definition of a dot is a little vague: I assumed that a dot is a fixed sized quantity, and hence that larger dots are actually several smaller dots stuck together.
My plan was to blow up the image, and create a grid of equally sized areas on it. Then I would count a sample, which would provide me an estimate, as well as some error bounds.
I'm assuming a model of the form
where D(A) denotes the number of dots for area A. If we double the area, then we double the number of dots. This assumption is visually compelling, but it's possible that we might discover that there is clumping of dots at certain scales, for example. Such clumping would invalidate the assumption on those scales. (This is an assumption which we could test statistically.)
I found it convenient to divide the region into 144 "equally sized" squares.
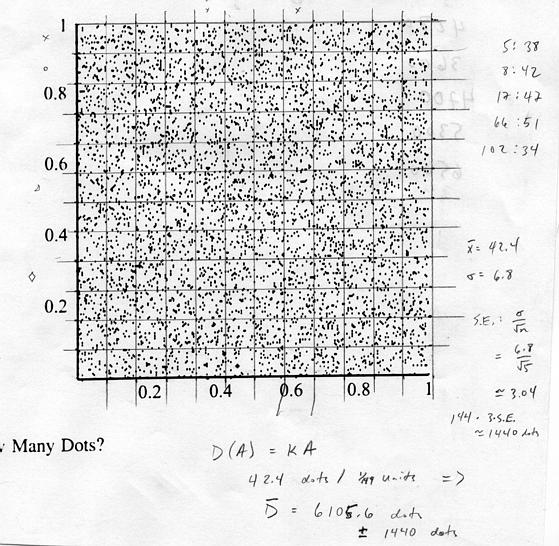
Rather than count all, I decided to count 5 squares (a small sample!), and used a random number generator to choose them. I assumed that a dot has the size of the smallest dot I could see (the pixel size of the machine that produced the plot, I assumed), and when I encountered larger dots I attempted to figure out how many pixels they covered. Dots on the line were included about half the time.
I obtained values of 38, 42, 47, 51, and 34, with a mean of 42.4, with a standard deviation of 6.8. This gives a standard error of about 3.04. Using this and slightly more than three standard errors from the mean value (I took 10 as the range of the actual mean), my (conservative) estimate is
(note that the area of the entire region is 1 unit squared, so D(1)=6106).
The class produced the following estimates:
| 2400 |
| 3250 |
| 3312 |
| 3600 |
| 3925 |
| 4280 |
| 4700 |
| 5000 |
| 5300 |
| 6106 plus or minus 1440 dots |
| 6500 |
It's clear that my estimate is on the high side. The large error bar (1440 dots) puts it in line with two other estimates.
One serious problem which would lead to varying estimates is the definition of a dot: my "one-pixel" method did not necessarily share universal agreement.