A: Sorry to hear that you're struggling. Let's see if this hint helps: If you have a recurrence relation of the form
![]()
then
- To find fixed points, you solve for solutions of the equation x=f(x).
-
Suppose that one of the fixed points found is
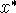 . To test
. To test 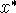 for
stability, check
for
stability, check 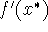 : if
: if 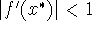 , then the
points is stable; if >1, unstable; if =1, neutrally stable (and the
graph and cobwebbing may make the case clear).
, then the
points is stable; if >1, unstable; if =1, neutrally stable (and the
graph and cobwebbing may make the case clear). - To do the cobwebbing, you simply bounce between the graphs of f and the line y=x, and see where fate leads you!
In example 3d, for example, the function f is
![]()
We solved ![]() for two roots (and hence two fixed points),
for two roots (and hence two fixed points), ![]() , and then tested the stability of each by visual inspection of
the graph:
, and then tested the stability of each by visual inspection of
the graph:
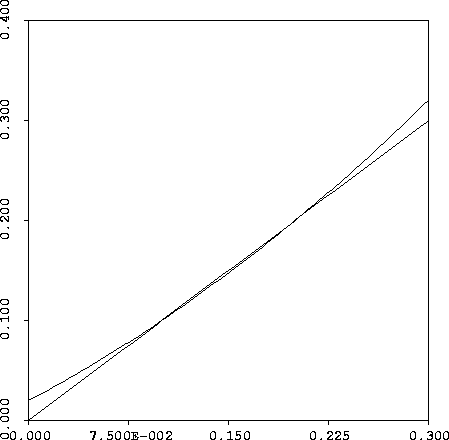
Figure 1: Graphs of y=x and f(x) intersect in two points (at .1
and .2).
We could also have tested their stability by computing
![]() :
:
![]()
so ![]() (.1 is a stable fixed point), whereas
(.1 is a stable fixed point), whereas
![]() (.2 is an unstable fixed point).
(.2 is an unstable fixed point).