Section 1.1: Statements, Symbolic Representations, and Tautologies

Abstract:

We encounter the elements of logic: statements, connectives, tautologies, contradictions, etc., and create wffs (``whiffs'') from these basic elements. An algorithm for detecting tautologies in the form of implications is described.

• Statement: a sentence possessing truth value (T or F).

  Exercise #1

• Logical connectives join statements into formulas, or compound statements:
  • conjunction (symbolized by 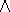, ``and'')
  • disjunction (symbolized by 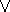, ``or'')
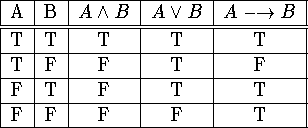
  • implication (symbolized by 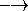: (does its table seem weird to you? It's by convention!)

    In the implication 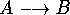, A is the antecedent, and B is the consequent. Some English equivalents to implication are given in Table 1.5.

    Exercise #4

     

    Implication plays an especially important role among connectives, so learn it well!

  • equivalence (symbolized by , ``if and only if'')
  • negation (symbolized by ', ``not'' - unary)
  Note: These connectives are not independent - some of these may be derived from the others (Exercise #22/29 shows that conjunction and negation suffice to write the others, for example).

  Exercise #6cde

  Example (more interesting): The dilemma of Protagoras and Eualthus.

• Well-formed formula (wff - "whiff") is a compound statement made up of statements, logical connectives, and other wffs What makes one well-formed?
  • Order of precedence:
    • parentheses
    • '
    • conjunction, disjunction
    • implication
    • equivalence

    Order of precedence helps us to simplify our lives: hence,

    

  • main connective (last to be applied)

• Truth table for a wff with n statement letters: rows

  Example: the table for implication above, which is a binary (2 statement letter) logical connective. Hence there are rows.

• tautology: wff which is always true (represented by 1).

• contradiction: wff which is always false (represented by 0).

• equivalent wffs: wffs A and B are equivalent, , if the wff

  

  is a tautology. (How can we prove that?)

  Some tautological equivalences:

  

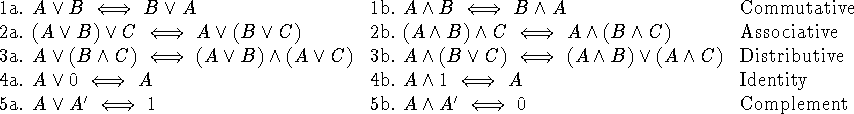
  Equivalent wffs will be useful when we are proving arguments, and want to replace complex wffs with simpler ones.

• De Morgan's Laws are two specific examples of equivalent wffs:
  • 
  • 
  Hence we claim that is a tautology.

  Exercise #15e/17e

  Notice that the two formulas appear analogous (``dual''). In fact, one is the negation of the other.

  Question: How so?

  Exercise #17/24

• Algorithm: a set of instructions that can be mechanically executed in a finite amount of time in order to solve some problem.

  Often written out in pseudocode, the author provides us an example: the algorithm TautologyTest is useful for whether or not an implication (that is, a wff where the main connective is implication) is, in fact, always true (a tautology). She proceeds by contradiction (one proof technique we'll study further in Chapter 2): assume that the implication is false. Then P must be true, and Q false (the only scenario which makes an implication false).

  Exercise 19/26: b,d

  Building a truth table for the implication also constitutes an algorithm to test to see if it is true, but, although the truth table algorithm may be more powerful (as more general, working for all would-be tautologies), TautologyTest may be faster when applied to an implication.