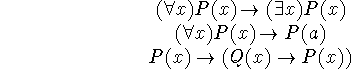Section 1.3: Quantifiers, Predicates, and Validity
Abstract:
We now throw variables into the mix, and investigate wffs which describe
properties of variables in given domains. We still test their truth values,
either for the specific domain in question, or even in all domains (validity).
-
quantifier: tells how many objects have a certain property.
Examples:
-
universal quantifier -
 - ``for all'', ``for every''
- ``for all'', ``for every'' -
existential quantifier -
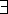 - ``there exists'', ``for at least one''
- ``there exists'', ``for at least one''
Have you encountered these quantifiers before?
-
predicate: a property of a variable (e.g. x prime)
We combine the quantifiers and predicates to create expressions such as

which we then must interpret. There is nothing special about the
variable x, so this wff is the same as 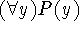 ,
, 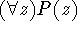 , etc. We say that x is a dummy variable.
, etc. We say that x is a dummy variable.
-
Truth value may now depend on the Interpretation of an expression:
-
domain of interpretation - non-empty set to which the predicate
expression is applied
-
assignment of a property of the objects to each predicate in the
expression
-
assignment of particular objects to each constant symbol in the
expression
Example: Ex. 4(b,d)
-
scope of a quantifier: the part of an expression to which the quantifier
applies; indicated with parentheses or brackets (but these may be neglected if
the scope is clear).
-
free variable: a variable in a predicate wff outside the scope of a
quantifier involving that variable.
Example: Ex. 5(c)
As noted before, this can be a very tricky business, but an important
one. Again, the process is not unique: there may be several different ways to
do the same job.
Example: Ex. 10/11(a-d)
-
Negation of predicate wffs: some cases are standard, e.g.
In general, English makes negation kind of tricky. Watch your step!
Example: Ex. 13/14(c,d)
The truth value of a predicate wff depends on the interpretation, but there are
some for which the wff is true independent of the interpretation. These are
called valid predicate wffs.
Whereas we can check the ``validity'' of a propositional wff (just check the
truth table to see if it's a tautology), there is no general check for the
validity of a predicate wff. In spite of that, there are some valid predicate
wffs, as demonstrated in the text:
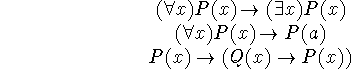
Example: Ex. 15/18(d,e)
LONG ANDREW E
Fri Aug 30 00:47:27 EDT 2002
 - ``for all'', ``for every''
- ``for all'', ``for every''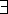 - ``there exists'', ``for at least one''
- ``there exists'', ``for at least one''
![]()
![]() ,
, ![]() , etc. We say that x is a dummy variable.
, etc. We say that x is a dummy variable.