Section 2.1: Proof Techniques

Abstract:

Sometimes we see patterns in nature and wonder if they hold in general: in such situations we are demonstrating inductive reasoning to propose a theorem, which we can attempt to prove via deductive reasoning. From our work in Chapter 1, we conceive of a theorem as an argument of the form , whose validity we seek to demonstrate.

This section outlines a variety of proof techniques, including direct proofs, proofs by contraposition, proofs by contradiction, proofs by exhaustion, and proofs by dumb luck or genius! You have already seen each of these in chapter 1 (with the exception of ``dumb luck or genius'', perhaps!).

Theorems and Informal Proofs

The theorem-forming process is one in which we

• make observations about nature, about a system under study, etc.;
• discover patterns which appear to hold in general;
• state the rule; and then
• attempt to prove it (or disprove it!).

This process is formalized in the following definitions:

• inductive reasoning - drawing a conclusion based on experience
• deductive reasoning - application of a logic system to investigate a proposed conclusion based on hypotheses (hence proving, disproving, or, failing either, holding in limbo the conclusion).
• counterexample - an example which violates a proposed rule (or theorem), proving that the rule doesn't work in general.

Before attempting to prove a theorem, we should be convinced of its correctness; if we doubt it, then we should pursue the line of our doubt, and attempt to find a counterexample.

Kids are wonderful at developing conjectures, and sometimes even applying deductive logic as illustrated by my friend's son Sam's Story. Practice 1, p. 85 illustrates the kinds of conjectures kids will make (e.g. ``All animals living in the ocean are fish.''), and parents, sibling, friend, and teachers all have the priviledge and pleasure of coming up with counterexamples.

Exhaustive Proof

Example: The Four-color problem

• Description (see p. 361/369).
• This theorem is partly famous because it provided the first example of a computer-aided proof of a major result. The reason the computer became useful was that the proof came down to testing a rather large number of special cases.

When there are only a few things (in particular, a finite number) to test, we can use proof by exhaustion.

Example: Prolog Prolog is able to test conjections, or theorems, such as in-food-chain(bear,algae) by simply doing a proof by exhaustion: it checks all cases, and eventually finds that algae is indeed in the bear's food chain.

Direct Proof

The most obvious, and perhaps common technique, is the direct proof: you start with your hypotheses , and proceed toward your conclusion Q:

Example: Exercise 7/9, p. 93/92

Contraposition

If isn't getting you anywhere, you can use your logic systems to rewrite it as (the contrapositive). This is called ``proof by contraposition''.

Example: Practice 4 and 5, p. 89

Example: Exercise 15/17, p. 93

Contradiction

Contradiction represents some interesting logic: again, we want to prove , but rather than proceed directly, we seek to demonstrate that : that is, that P and Q' leads to a contradiction. Then we cannot have both P true, and Q false - which would lead to false, of course.

Example: Exercise 19/22, p. 93

  
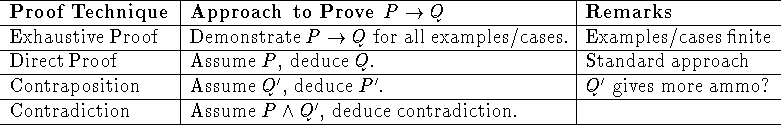
Table: Summary of useful proof techniques, from Gersting, p. 91.

Serendipity

Mathematicians often spend a great deal of time finding the most ``elegant'' proof of a theorem, or the shortest proof, or the most intuitive proof. We may stumble across a beautiful proof quite by accident (``serendipitously''), and those are perhaps the most pleasant proofs of all. There is a wonderful story associated with Exercise 50/55, p. 95/94.