Exercise 7/9, p. 93/92

Prove: the sum of even integers is even.

Proof: Given a pair of even integers m and n, which can be written as 2i and 2j, where i and j are integers. Consider the sum m + n: m + n = 2i + 2j, or 2(i+j). Since 2 is a factor of this integer, the sum m + n is also even. Q.E.D.

Practice 4 and 5, p. 89/88

1. If the river doesn't flood, then the rain will stop.
2. If the network is up, then the central switch is up.
3. If the avocados are not both dark and soft, then they aren't ripe.
4. A bad diet leads to a sick cat.

1. If the river floods, then the rain will continue.
2. If the network is down, then the central switch is down.
3. If the avocados are not dark and soft, then they are ripe.
4. A good diet leads to a healthy cat.

Exercise 15/17, p. 93

Prove: If a number x is positive, so is x+1.

Proof: In this case, P(x) is the statement ``x is positive'', and Q(x) is ``x+1 is positive''. To prove by contraposition, we attempt to prove that, if x+1 is not positive, then x is not positive. Hence, assume that x+1 is not positive (i.e., ). Then , which implies that x is not positive.

Exercise 19/22, p. 93

Prove: If x is an even prime number, then x=2.

Proof (by contradiction): Suppose that x is an even prime, but that . Then x=2k, where k is an integer greater than 1. But this contradicts the fact that x is prime!

Exercise 50/55, p. 95/94

Prove: The sum of the integers from 1 to 100 is 5050.

Since this is simply a sum, we need only add up the numbers. Gauss was a precocious student, and his teacher, to amuse him for a long time, gave him this exercise when he was but a young school boy. Unfortunately for the school master, Gauss was back at his desk a few minutes later with the answer.

Proof (by ``serendipity''): Gauss broke the integers into pairs, and added them together:

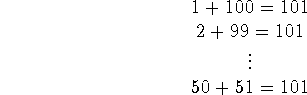
and there are 50 such pairs, so the sum is 5050.