Section 2.2: Induction

Abstract:

In this section we investigate a powerful form of proof called induction. This is useful for demonstrating that a property, call it P(n), holds for all integers n greater than or equal to 1.

Actually, the ``1'' above is not essential: any ``base integer'' will do (like 0, for example: it really only matters that there be a ``ground floor'', or ``anchor'').

Induction

Induction is a very beautiful and somewhat subtle method of proof: the idea is that we want to demonstrate a property associated with natural numbers (or a subset of the natural numbers). As a typical example, consider a theorem of the following type:

Prove that, for any natural number n, (Gauss's theorem, stated when he was five or so).

An induction proof goes something like this:

• We'll show that it's true for the first case (usually k=1, called the base case). While the first case is often k=1, this isn't mandatory: we simply need to be sure that there is a first case for which the property is true.
• Then we'll show that, if the property is true for the case, then it's true for the case (the induction step).
• Then we'll put them together: if it's true for 1, then it's true for 2; if it's true for 2, then it's true for 3; .... ``to infinity, and beyond!'' Or up the ladder, as our author would say.

Imagine dominoes falling. That's what it's like.

The most commonly used form of the principle of induction is expressed as follows:

First Principle of Mathematical Induction:

or, more succinctly,

where the domain of the interpretation is the natural numbers. This is just modus ponens applied over and over again!

Vocabulary:

• inductive hypothesis: P(k)
• basis step (base case, anchor): establish P(1)
• induction step (implication):

Example: (practice 7, or ``Gauss's theorem'') Prove that, for any natural number n, .

Example: Exercise 30/34: Prove that for .

A second (and seemingly more powerful) form of induction is given by the Second Principle of Mathematical Induction:

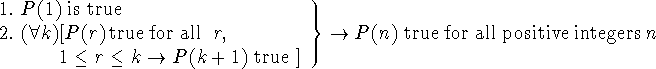
This principle is useful when we cannot deduce P(k+1) from P(k) (for k alone), but we can deduce P(k+1) from all preceeding integers, beginning at the base case.

Example: Exercise 60/64b, p. 110/109.

Each of these two principles is equivalent to the Principle of Well-Ordering, which states that every collection of positive integers that contains any members at all has a smallest member.

Example: Prove that the first principle of induction implies well-ordering (Exercise 68, p. 186 - not in Edition 5!).

A Final Example: The prisoner's last request (finite backwards induction!)