denotes inclusion in a set, so that 
means that x is a member (or element) of a set, and 
means
that x isn't a member.
This section, the only section we consider from Chapter 3, simply gives us some basic vocabulary and notions of sets that we will need when we get to Boolean algebras later. It also includes some really interesting examples of ideas from set theory (e.g. different sizes of infinite sets - did you know that infinity comes in infinitely many different sizes?).
A set (call it A) is loosely a collection of objects.
Capital letters denote sets, and denotes inclusion in a set, so that means that x is a member (or element) of a set, and means
that x isn't a member.
Sets are unordered: the order in which the elements are listed is unimportant.
We use predicate logic to determine when two sets are equal:
The notation for a set whose elements are characterized by possessing property P is
and is read ``S is the set of all x such that P(x)''
One curiously useful set is the empty set, denoted 
or 
.
Some important sets of numbers:
Example: Practice 3, p. 163/165
A is a subset of B, denoted 
, if
and A is a proper subset of B, denoted 
, if
Example: Practice 6, p. 164/166
Theorem:
Power Set: Given set S, the power set of S, denoted 
, is the
set of all subsets of S. (Note that S and are elements of the
power set of S.)
Example: How big is the power set of a given set? (Practice 9, p. 166/168)
We can create ordered pairs of elements of a set. From 
we can create the ordered pairs (1,3) and (3,3), for example. Now the
order of the elements is important!
Question: How many ordered pairs are there if we have a set with n elements?
Definition: 
is a binary operation on a set S if for
every ordered pair (x,y) of elements of S, 
exists, is unique,
and is a member of S.
Definition: is well-defined if exists and is unique.
Definition: is closed if 
.
Three ways to fail to be a binary operation on S:
fails to exist; gives multiple different results; doesn't belong to S.
Definition: a unary operation on a set S associates with every element x of S a unique element of S.
Example: Practice 12, p. 168/170
Given a set S of elements of interest, we may want to operate on various
subsets of S (that is, elements of ). For example,
Definition: Let 
.
The union of A and B, denoted 
, is given by 
.
The intersection of A and B, denoted 
, is given by 
.
Venn Diagrams are useful tools for considering the notions of union and intersection. The diagrams in Figures 3.1 and 3.2 (p. 169/171) illustrate these notions ``pictorially''.
Definition: For a set 
, the complement of A,
denoted A', is 
.
Example: Practice 14, p. 170/171: illustrate A' using a Venn Diagram.
Definition: For set , the set-difference of A
and B, denoted A-B, is given by 
.
Definition: For set , the Cartesian product (cross
product) of A and B, denoted 
, is the set of all ordered
pairs, and is given by
Example: Practice 15, p. 170/172: illustrate A-B using a Venn Diagram.
We will encounter the following ``Set identities'' later in the context of Boolean algebras:
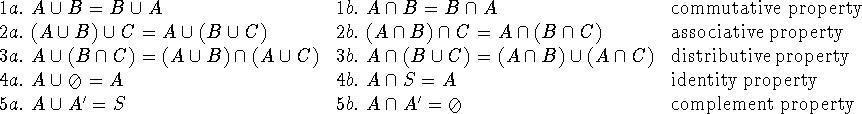
Notice the ``dual'' nature of the properties: it seems that the operations of
and 
have a lot in common!
Question: What correspondence do you observe between these identities
and those of wffs with the logical connective 
and 
?
As an interesting application of set theory, we will now demonstrate that there are various sizes of infinity!
The natural numbers comprise the smallest infinity, a denumerable or countable infinity.
We prove that two sets are of equal size (even if infinite!) by creating a one-to-one correspondence between the two sets. If such a correspondence exists, then the two sets have the same size.
Theorem: the rational numbers are denumerable.
Theorem: the real numbers are not denumerable.
Theorem: the power set of a set S is always larger than S (punch line: there is always a bigger infinity than the one you already have).