There are several different ways to represent a graph in a computer.  Although graphs are usually shown diagrammatically, this is only possible when the number of vertices and edges is reasonably small.

    Graphs can also be represented in the form of matrices.  The major advantage of matrix representation is that the calculation of paths and cycles can easily be performed using well known operations of matrices. However, the disadvantage is that this form of representation takes away from the visual aspect of graphs.  It would be difficult to illustrate in a matrix, properties that are easily illustrated graphically.
 

Example:  Matrix representation of a graph

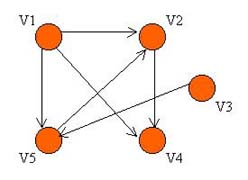
    Consider the following directed graph G (in which the vertices are ordered as v₁, v₂, v₃, v₄, and v₅), and its equivalent adjacency matrix representation on the right:

v1 v2 v3 v4 v5 v1 0 1 0 1 1 v2 0 0 0 1 0 v3 0 0 0 0 1 v4 0 0 0 0 0 v5 0 1 0 0 0

    As you can see from the above graph, if a path of length 1 exists from one vertex to another (ie. the two vertices are adjacent), there must be an entry of 1 in the corresponding position in the matrix.  For example, from the vertex v1, we can reach vertices v2, v4, and v5. Therefore, we have a corresponding entry of 1 in the matrix in the first row and the second, fourth and fifth columns.

    In general, the number of 1's in the ith row, corresponds to the number of edges leaving the vertex v_i, and the number of 1's in the jth column, corresponds to the number of edges entering the vertex v_j.
 

Definition of an Adjacency Matrix

    An adjacency matrix is defined as follows:  Let G be a graph with "n" vertices that are assumed to be ordered from v₁ to v_n.
The n x n matrix A, in which

           a_ij= 1        if there exists a path from v_i to v_j
            a_ij = 0        otherwise

is called an adjacency matrix.
 

Calculating A Path Between Vertices

    As shown in the previous example, the existence of an edge between two vertices v_i and v_j is shown by an entry of 1 in the i^th row and j^th column of the adjacency matrix.  This entry represents a path of length 1 from v_i to v_j.

    To compute a path of length 2, the matrix of length 1 must be multiplied by itself, and the product matrix is the matrix representation of path of length 2.
 

Example:  Computing A Matrix Representation of Path of Length 2

   Using the matrix from the previous example and multiplying it by itself, we obtain the following new matrix:
 

Original Graph G:

Matrix representation of path of length 2 v1 v2 v3 v4 v5 v1 0 1 0 1 0 v2 0 0 0 0 0 v3 0 1 0 0 0 v4 0 0 0 0 0 v5 0 0 0 1 0

    The above matrix indicates that we can go from vertex v1 to vertex v2, or from vertex v1 to vertex v4 in two moves.  In fact, if we examine the graph, we can see that this can be done by going through vertex v5 and through vertex v2 respectively.  We can also reach vertex v2 from v3, and vertex v4 from v5, all in two moves.

    In general, to generate the matrix of  path of length n, take the matrix of path of length n-1, and multiply it with the matrix of path of length 1.

Click here to see how matrix multiplication is done.
Click here to see an interactive example of an Adjacency Matrix.
Or move on to the next page to go directly to the next section.

Back to Terminology: Paths, Reachability, Connectedness

On to Graph Representation: Adjacency Lists