Some examples are provided in gory detail.
Exercise #3, p. 437/441
In this case, we're using Dijkstra's algorithm. We start with the adjacency matrix:
The adjacency matrix serves the computer to indicate which nodes are adjacent to which others.
Now, we're going to keep track of the ``settled nodes'', starting with the
initial node ( 
). We will also keep track of their distances to node
1, and we'll keep a list of their nearest neighbor along their shortest path
back to 1. They start this way, therefore:
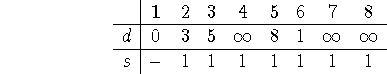
Note that once a node is settled, its entries won't be changing.
The next closest node is 6: it is one unit away from 1. Any other node must be
further away, as to go directly from 1 requires more than 1 unit, and passing
by node 6 would still be farther than one unit (one unit and change). Hence 6
is added to 
, and
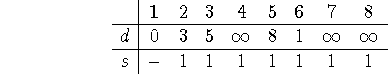
Since node 6 has neighbors 
, these are the only nodes whose
distances could be updated. Node 1 will change, however, as it is already
settled in for its long winter's nap. Looking the others over, we see that
there are some improvements to both 5 and 7:
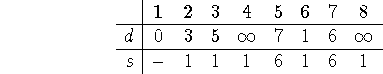
We now settle 2, with neighbors 
, of which only 3 and 7 can change:
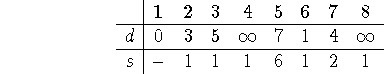
Node 3 sticks, but 7 can be reached in only 4. This makes it our next settled
node, with neighbors 
: only 8 can still change! And it does:
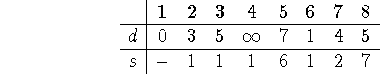
We now take 3 as our next settled node, although the choice is arbitrary (both
3 and 8 are at distance 5). Node 3 has neighbors 
, so only 4 and 8
can change (and only 4 does):
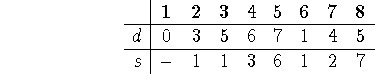
Now node 8 is settled, whose neighbors are 
. Only 5 can change, and
it does:
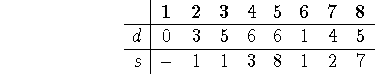
Now, if our algorithm is smart, it will decide ties in favor of the destination node. So let's assume a smart algorithm: then the next settled node will be node 5, our final destination. The arrays end, then, as
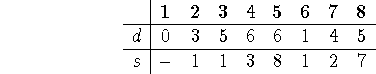
which indicates that the shortest path between nodes 1 and 5 has length 6, and the path is given by the s array: 5's adjacent neighbor on the path to 1 is 8; 8's is 7; 7's is 2; and 2's is 1. Hence the shortest path is
This algorithm allows us to find the shortest distance from the initial node to all other nodes, and is hence a generalization of Dijkstra's algorithm.
We're going to compute shortest paths of 1 arc, 2 arcs, ..., (n-1) arcs, which are the longest paths we would possibly use to get to any node from 1 (otherwise we would be visiting a node twice, which would be foolish!).
Exercise #10/12, p. 439/443
Fortunately we're using the same graph, so the adjacency matrix is essentially the same. We start with the adjacency matrix
with zeros down the diagonal in place of the infinities before.
We essentially add each row of the adjacency matrix to the current d vector, and check to see if we get any improvement. If so, we've found a shorter path! d contains the shortest distances determined so far from the initial node to every node in the graph.
Once again we're going to keep track of the distances from the initial node, starting with the initial node 1. We will also keep track of their nearest neighbor along their shortest path back to 1. They start this way, therefore:
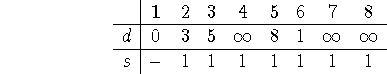
Only when a node changes will it impact other nodes. We now ask about paths using two arcs: what are the shortest distances for each node from node 1? In order to answer this question, you need to examine each node's neighbors (use the adjacency matrix!), and check their nearest distances. Again, if these neighbor distances have not changed from one step to the next, then the distance to the given node will not change either!
At the second iteration, paths of two arcs, our distances look like this:
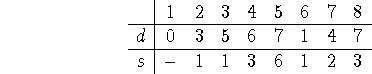
For example, if we add the fourth node's row of the adjacency matrix to the original d array, we get
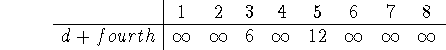
which says that we can get to node 4 in 6, using node 3. We do the same for all the other nodes (other rows of the adjacency matrix).
Iterate: we again step through the rows, checking the neighbors of each node against their newly calculated values to see if there's any improvement. Only for node 8 do we see any change:
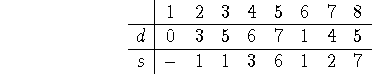
Node 8's only neighbors are , so only these can change in the next
step: we use their rows from the adjacency matrix, and try again:
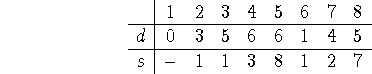
Only 5 changed. It's neighbors are 
, but none of them
change. Hence we are done! There can be no further change.
The d array gives us the nearest distances to 1 for each node, and their paths can be calculated exactly as for Dijkstra's algorithm.
Exercise #13/15, p. 439/444.