, and one unary operation ', and in which
there are two distinct elements 0 and 1 such that the following properties hold
for all 
:
First of all, note that we're only reading 7.1 through p. 473/468 (up to Isomorphic Boolean Algebras).
A Boolean algebra (named after George Boole) is a generalization and an abstraction of the propositional logic we studied early this term, as well as the set theory which we glanced at. We are really interested in using it to understand the basic elements of computer logic, however, which is based on a binary (0,1) alphabet. In this first section we are merely introduced to the fundamental concepts of Boolean Algebra.
Definition: a Boolean Algebra is a set B on which are defined
two binary operations + and , and one unary operation ', and in which
there are two distinct elements 0 and 1 such that the following properties hold
for all :
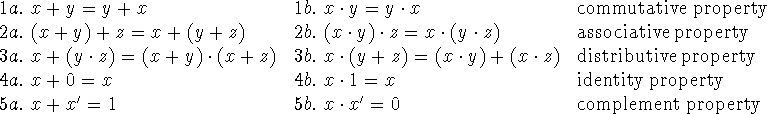
The element x' is called the complement of x. The algebra may be
denoted 
.
Of these properties, certainly the distributive property 3a. may seem the
strangest, since it obviously doesn't hold for the usual suspects + and .
Notice the beautiful symmetry in this definition: the roles of + and
are exactly reversed with respect to the special elements 0 and 1.
Question: how are these reflected in the properties of propositional logic that we studied earlier this term?
, and example (implication).
and =....
In Example 2, p. 470/465, the set 
consisting of only two
elements (so they must be our distinguished elements), and the binary
operations of
+ by x+y=max(x,y)
and that of
by
.
Complements are given by 0'=1 and 1'=0. It turns out that this is another
example of a Boolean Algebra.
Practice 1, p. 471/465.
Curiously enough, x+x=x in a Boolean Algebra (this is the idempotent
property. You'll want to remember that one, for proofs! And since x+x=x, we
must have 
by the beautiful symmetry of the operations. This idea,
known as duality, means that we only have to do half the work most of
the time....
You may have bumped into this concept in linear algebra: for example, projection matrices are idempotent, such as
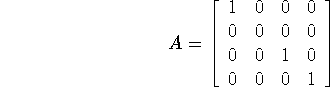
This matrix projects onto the first, third, and fourth dimensions; and
projecting onto those dimensions a second time doesn't change anything (i.e.,
).
Practice 2, p. 472/467.
Given an element x of the set B of a Boolean Algebra, the complement x' is the unique element of B with the property that
Practice 3, p. 472/467.
Hints for proving Boolean Algebra Equalities:
) or multiplying by some form
of 1 (like x+x').
Exercise 7/8, p. 481/475
Exercise 10/11a, p. 481/476