The word ``minimization'' in the title of this section refers to our pursuit of simplified but equivalent Boolean expressions, which we think of as representing hardware (logic networks). Our objective is to start with the canonical form derived from a truth table, and reduce it to a simpler expression (generally also a sum of products), which is easier (cheaper, faster) to implement in hardware.
We examine two different techniques for accomplishing this: the Karnough map, and the Quine-McCluskey procedure. The first is aesthetically pleasing, but limited to a few boolean variables; the second can be generalized to handle any number of variables, and can be coded up in general relatively easily.
In Section 7.2, we discovered that there is a relatively simple way of passing back and forth between representations of a truth function (table), boolean expression, and logic network. In particular, we saw that, given a truth table, it is simple to construct a Boolean expression (the canonical form) which is a sum of products. Unfortunately, this expression is often much more complicated than necessary - it can be simplified, or minimized.
In this section, we consider two methods for dealing with truth tables, and turning them into simple Boolean expressions. The Karnough Map turns a truth table into an equivalent ``matrix'', which we operate on; and the Quine-McCluskey procedure plays a similar pattern-matching game, making selective deletions to trim down the canonical form to a manageable Boolean expression.
A couple of simple equivalence rules make our life easy:
![]()
We demonstrate the utility of these two rules in the following simplification:
Example 17, p. 509/500. Consider the canonical form given by
![]()
We demonstrate how rule (1) works as follows:
![]()
Now we're set up for the use of rule (2):
![]()
To demonstrate rule (2) above, we get to use that wacky distributive rule:
![]()
Here's a two-variable example (XOR - from the half adder of last time):
![]()
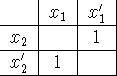
Example 17: ![]()
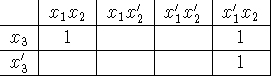
While the position of the boolean variables in the 2x2 example above is arbitrary, not so for the column labels of the 3x3 example above: notice that there is a single change in the Boolean expressions as you read across the top. Note also that the far left and right expressions are also only different by one change. We could wrap this table and put it onto a cylinder.
A four-variable example.
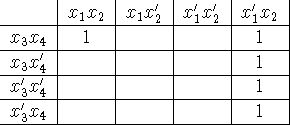
In this case, there is nothing arbitrary about either row- or column-labels: you could wrap top to bottom and right to left, which means that this table could be wrapped onto a torus (or donut shape).
In this section we study a method for simplification, not just representation, so how do we simplify?
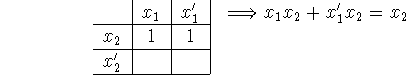
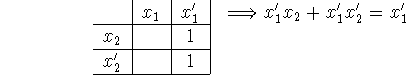
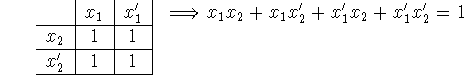
Check out this trick (idempotence):
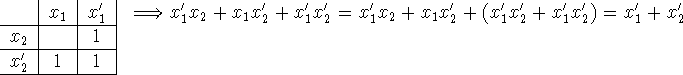
Notice, however, that this is really the same as rule (2) above:
![]()
Example 17: ![]()

Note that we need to wrap to do this one; furthermore see how much more simply we simplify this expression than we did up top: we use idempotence, then the simplification rule (1) twice (not needing the second).
There may be multiple simplifications of a Boolean expression:
Exercise #1, p. 523/512
We may need to look for quads, rather than pairs:
Exercise #4, p. 523/512
In this procedure, we do exactly the same thing as in Karnough, but we do it without the matrix (or table). We search for those elements of the truth table which differ by a single entry, and then reduce them.
We may have to do the reduction in several steps, as illustrated in Table 7.16, p. 520/509. Part (c) of that table represents a square of four 1s in the Karnough map.
In the end, we have to determine which of the resultant products is necessary to recreate the initial truth table. We do this with a second type of table, as illustrated in Table 7.17, p. 520. This is essentially a pattern-matching table (we'll talk about these pattern-matches in our discussions of regular expressions in section 8.2): each of the column label expressions (the original product terms) is compared to the ``deleted elements'' of the result tables (e.g. the product 0010 matches both 0-10 and 00-).
Exercise 14/16, p. 522/514.
Furthermore, it is sometimes easier to use the Quine-McCluskey procedure on the complement of the truth function, if the complement has fewer 1 entries.
Exercise 17/19, p. 527/515 (or Exercise 14/16 above, for a simpler example).