Overview of Chapters 3.1, 5, 6, and 7.1
Abstract:
Your test will resemble the problems from your homework assignments.
You will probably have 10 smaller, equally weighted questions or so (one every
5 minutes!), one of which will involve several true/false questions (like the
self-tests at the end of each chapter - answers are at the end of the book).
-
The notation of sets (definition, order, cardinality, empty set, power set,
Cartesian products, countable, uncountable, ...)
-
Using predicate logic to determine when two sets are equal
-
Relationships between sets
-
binary and unary operations (and conditions for their proper definition)
-
intersection, union, complements, set-difference, and Venn diagrams
-
one-to-one correspondence, and proving that cardinalities are the same.
-
tree: an acyclic, connected graph with one node designated as the
root node (or defined recursively).
-
tree terminology
-
examples of trees
-
tree representations
-
tree traversal algorithms:

-
decision tree: a tree in which
-
internal nodes represent actions,
-
arcs represent outcomes of an action, and
-
leaves represent final outcomes.
-
Examples
-
Lower Bounds on Searching
-
Binary Search Tree (Binary Tree Search)
-
Sorting
-
Theorem on the lower bound for sorting: you have to go to at least a depth of
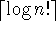 in the worst case.
in the worst case.
-
Euler Path: a path in which each arc is used exactly once.
-
Theorem: in any graph, the number of odd nodes (nodes of odd degree) is
even.
-
Theorem: an Euler path exists in a connected graph
 there are
either two or zero odd nodes.
there are
either two or zero odd nodes. -
Using the EulerPath algorithm (simply counts up elements in a row i of
the matrix (the degree of node i), and checks whether that's even or odd; if
in the end there are not zero or two even nodes, there's no Euler path!)
-
Hamiltonian Circuit: a cycle using every node of the graph.
-
Shortest Path algorithms (for a simple,
positively weighted, connected graph)
-
Dijkstra's Algorithm
-
Bellman-Ford Algorithm
-
Floyd's algorithm
-
Minimal Spanning Trees:
A spanning tree for a connected graph G is a non-rooted tree
containing the nodes of the graph and a subset of the arcs of G.
A minimal spanning tree is a spanning tree of least weight of a simple,
weighted, connected graph G.
-
Prim's algorithm
-
Kruskal's algorithm
Traversing a graph (generalizes tree traversal):
-
depth-first strategy
-
breadth-first strategy
Remember: for the test stick with the convention that, given a choice,
we should choose nodes in alphabetic order.
-
How Boolean Algebras generalize propositional logic and set theory.
-
The definition, and verifying that
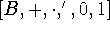 is a Boolean algebra
is a Boolean algebra -
Additional rules, such as De Morgan's laws, and idempotence.
-
Duality
-
Proving Boolean algebra equalities
LONG ANDREW E
Fri Nov 22 01:53:39 EST 2002
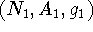 and
and 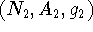 are
isomorphic if there are bijections (one-to-one and onto mappings)
are
isomorphic if there are bijections (one-to-one and onto mappings)
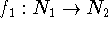 and
and 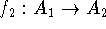 such that for each arc
such that for each arc 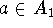 ,
,
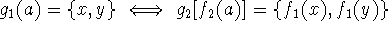 (replace braces by
parentheses for a directed graph).
(replace braces by
parentheses for a directed graph).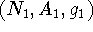 and
and 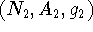 are
isomorphic if there is a bijection
are
isomorphic if there is a bijection 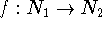 such that for any nodes
such that for any nodes
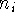 and
and 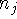 of
of 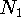 ,
, 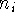 and
and 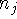 are adjacent
are adjacent 
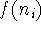 and
and
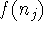 are adjacent.
are adjacent.![]()
