
On this problem in part a, I had hoped that you would simply observe that these were the operations of propositional logic; in part b, that an element being its own inverse reduces a set of 4 elements to 1. Nice job by this student.

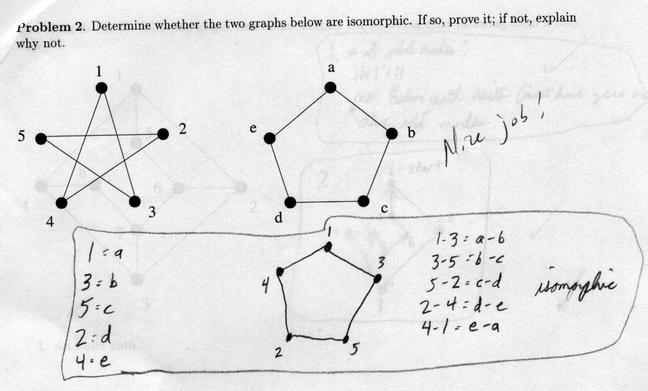
You need to do more than provide a bijection - you need to tell me what the bijection does for me! This student provided the bijection (rather informally, but okay) at left, then shows that it takes arcs into arcs in the correct way (at right).

This student of Problem 3 got lucky: I should have noticed that part 2 has a "union" where an "intersection" is required.
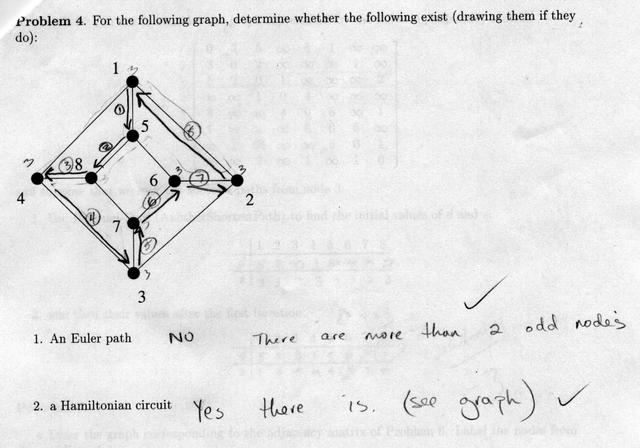


This was the only paper on which the fact that there were two choices for node 7 was made. Good job! Again, this student indicated that s/he knew what s/he was doing by the "1 arc", "2 arc" notations. Keep me informed of what you're doing!
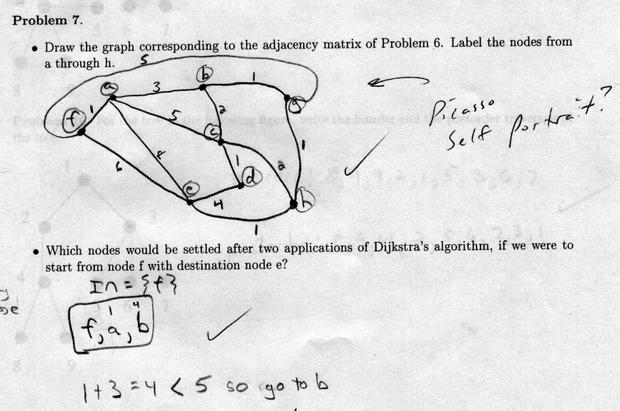
I like the drawing above, because this graph is, in fact, planer - it can be drawn without superfluous intersections. I should have given extra credit....
The explanation of how the nodes are settled is a little cryptic, but certainly shows that the student knew what s/he was doing.

My bad on problem 9: I have "tree" where I should have "graph" (teach me to cut and paste!? Naaah!). As one student pointed out following the test, this throws part 3 of problem 8 into question - since the "tree" in problem 9 is cyclic - but my feeling is that you shouldn't be swayed by me into saying something false. Stand by your convictions! By definition, a tree is acyclic.