Section 8.2: Finite-State Machines

Abstract:

We model a machine as a set of states, inputs which lead to a change in state, a clock to synchronize the machine world, and outputs, which result from a particular state. We use tables and graphs to describe how the inputs relate to changes in state and the outputs of each state, then practice creating simple finite-state machines.

Finite-state machines can be used to recognize input, and we will look at the kinds of input that can be recognized, as well as construct the machines that recognize given input. Furthermore, some machines are overly complicated, in that we can simplify them and get the same operation. We will examine some ways in which we can ``minimize'' a finite-state machine.

Finite-State Machines

Definition: A finite-state machine M is a structure where

  
Table: Elements of a finite-state machine.

We assume discrete times, synchronized by a clock, so that

and that

We represent and by

• state tables (e.g. Table 8.1, p. 560/545)
• state graphs (e.g. Figure 8.1, p. 560/546)

A summary of these elements for Example 16, p. 559/545:

  
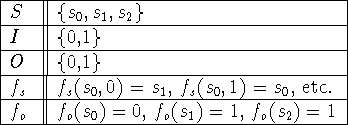
Table: Elements of finite-state machine of Example 16, p. 559/545.

Practice 35, p. 561/546. (Table from graph: first of all, what are in this example?)

Practice 36, p. 561/546.

Practice 34, p. 561/546.

Exercise 4, p. 576/563.

Construction of a machine: the Binary Adder

Note: major goof - the fourth sum at the bottom of page 561 of the 4th edition is wrong: We know that 1+1=10 in binary!

In section 7.2 we saw how one might create a logic network in hardware for the addition of binary numbers. We now consider how this can be incorporated into a finite-state machine which is analogous (p. 561/547).

We must specify the five elements of a finite-state machine: . What is the set of states, what the set of inputs, what the set of outputs, and how are the functions and defined?

Practice 37, p. 562/547

Practice 38, p. 563/548

Now let's try something a little different:

Exercise 13/15(a), p. 578/565 (I don't like the way the author's solution machine looks in the back of the book!)

Recognition

Definition: Finite-State Machine Recognition A finite-state machine M with input alphabet I recognizes a subset S of (the set of finite-length strings over the input alphabet I) if M, beginning in state and processing an input string , ends in a final state (a state with output 1) if and only if .

Practice 40, p. 565/550

Notes:

• Note the emphasis on the word ``ends'': we assume that the input stops, and when the input stops the final output is a 1.
• Note also the ``if and only if'': this indicates that, if the output ends in a 1, then the string is in S; and if string is in S, then the output ends in a 1.

What kinds of input can a finite-state machine recognize? Regular expressions. Regular expressions over I are defined recursively by

1. the symbol and the symbol ;
2. the symbol i for any ; and
3. the expressions (AB), , and if A and B are regular expressions.

Kleene's Theorem assures us that a finite-state machine can recognize a set S of input strings if and only if the set S is a regular set (that is, a set represented by a regular expression).

Since some very reasonable sets are not regular (e.g. , where stands for n copies of a), finite-state machines are obviously not sufficient to understand all of computation.

Examples of regular sets given by regular expressions:

• #18b. The set of all strings beginning with 000:
• #18e. The set of all strings ending in 110:
• #18f. The set of all strings containing 00:
• #18d. The set of all strings consisting entirely of any number (including none) of 01 pairs or consisting entirely of two 1s followed by any number (including none) of 0s:
• #25b. The set of all strings of 0s and 1s having an odd number of 0s: .

Exercise 17/19(e), p. 579/566 - recognition and minimization motivation

Machine Minimization

Unreachable States

One obvious way in which a machine can be minimized is if there is an unreachable state: if so, then that state can certainly be trimmed from the machine without any consequences (from the standpoint of output). For example: Table 8.3, p. 568/552; and Figure 8.7, p. 568/553.

Practice 43, p. 568/553

Equivalent States

It would be nice if we had some general way of minimizing a machine, however. It turns out that we can find a minimized machine by using the idea of equivalent states. The idea is that several redundant states might operate in such confusing fashion that it appears there's lots going on, when there's not!

In the first step, the unreachable states are removed. That's the easy part! Then we define

Equivalent States: two states and of M are equivalent if, for any , where by the awful notation we mean the sequence of output which occurs given that we start in state s and receive input .

(There is no way that our author should have used notation which seems to imply that is somehow both a function from and a function from , except that she's proving herself a computer scientist and an object-oriented one at that, and overloading the function ...).

In order to find equivalent states, we define the notion of k-equivalency: two states are k-equivalent if the machine matches output on an input of k symbols to the two states.

1. States having the same output symbol are 0-equivalent.
2. For 1-equivalency, we check two states to see that the next-states under all input symbols (of length 1) are 0-equivalent.
3. Etc.!

We iteratively step through equivalencies (from 0 on up): as soon as the states do not change, from k-equivalency to (k+1)-equivalency, then we have minimized our machine.

Best to look at an example!

Exercise 34/41, p. 584

The set of states is divided up into subsets of the initial set which have for their union the entire set S, and no common intersections. This is called a partition of the set S. As we progress from 0-equivalency on up, each subset can be divided, but none ever coalesce. There can be partition refinement (finer partition) only.