Exercise 12, p. 93

Prove: the sum of an integer and its square is even.

Proof: Given an integer n and its square, . Consider the sum : , which is the product of consecutive integers. If n is even, then the product is even; if n is odd, then (1+n) is even, so the product is even. Q.E.D.

Practice 4

1. If the river doesn't flood, then the rain will stop.
2. If the network is up, then the central switch is up.
3. If the avocados are not both dark and soft, then they aren't ripe.
4. A bad diet leads to a sick cat.

Practice 31

Exercise 15, p. 93

Prove: If a number x is positive, so is x+1.

Proof: In this case, P(x) is the statement ``x is positive'', and Q(x) is ``x+1 is positive''. To prove by contraposition, we attempt to prove that, if x+1 is not positive, then x is not positive. Hence, assume that x+1 is not positive (i.e., ). Then , which implies that x is not positive.

Exercise 19, p. 93

Prove: If x is an even prime number, then x=2.

Proof (by contradiction): Suppose that x is an even prime, but that . Then x=2k, where k is an integer greater than 1. But this contradicts the fact that x is prime!

Exercise 50, p. 95

Prove: The sum of the integers from 1 to 100 is 5050.

Since this is simply a sum, we need only add up the numbers. Gauss was a precocious student, and his teacher, to amuse him for a long time, gave him this exercise when he was but a young school boy. Unfortunately for the school master, Gauss was back at his desk a few minutes later with the answer.

Proof (by ``serendipity''): Gauss broke the integers into pairs, and added them together:

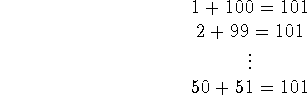
and there are 50 such pairs, so the sum is 5050.