Section 2.2: Induction

Abstract:

In this section we investigate a powerful form of proof called induction. This is useful for demonstrating that a property, call it P(n), holds for all integers n greater than or equal to a base integer (which we will take to be 1, for our discussion - but it really only matters that there is a ``ground floor'', or anchor).

Induction

Induction is a very beautiful and somewhat subtle method of proof: the idea is that we want to demonstrate a property associated with natural numbers (or a subset of the natural numbers). As a typical example, consider a theorem of the following type:

Prove that for .

An induction proof goes something like this:

• We'll show that it's true for the first case (usually k=1, called the base case). While the first case is often k=1, this isn't mandatory: we simply need to be sure that there is a first case for which the property is true.
• Then we'll show that, if the property is true for the case, then it's true for the case (the induction step).
• Then we'll put them together: if it's true for 1, then it's true for 2; if it's true for 2, then it's true for 3; .... ``to infinity, and beyond!''

The most commonly used form of the principle of induction is expressed as follows:

First Principle of Mathematical Induction:

Vocabulary:

• basis step (base case, anchor): establish P(1)
• induction step (implication):
• inductive hypothesis: P(k)

Example: Prove that, for any natural number n, .

Example: Exercise 30: Prove that for .

A second (and seemingly more powerful) form of induction is given by the Second Principle of Mathematical Induction:

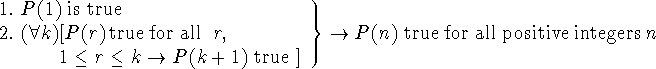
This principle is useful when we cannot deduce P(k+1) from P(k) (for k alone), but we can deduce P(k+1) from all preceeding integers, beginning at the base case.

Example: Exercise 60, p. 110.

Each of these two principles is equivalent to the Principle of Well-Ordering, which states that every collection of positive integers that contains any members at all has a smallest member.

Example: Proof that the first principle implies well-ordering (Exercise 68, p. 186).

A Final Example: The prisoner's last request (finite backwards induction!)