Section 5.1, part A: Graphs and their representations

Abstract:

In the first few pages of section 5.1 (through p. 341, Planer Graphs), we are introduced to definitions of graphs, various kinds of graphs, characteristic features of graphs, and even a few theorems about graphs.

Definitions

A graph is defined loosely as a set of nodes, and a set of arcs which connect some of the nodes.

Question: how does this jive with our understanding of a graph from calculus? For example, the graph of ?

More formally, we have the following

Definition: a graph is an ordered triple (N,A,g) where

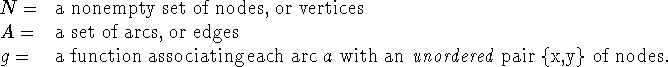
x and y are the endpoints of the arc. g is a function and .

Question: how does this jive with our understanding of the graph of ?

To do: Practice #1, p. 331.

Definition: a directed graph is an ordered triple (N,A,g) where

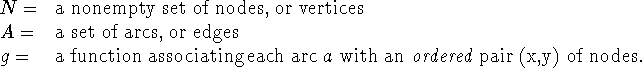
so g is a function and .

Question: how does this jive with our understanding of the graph of ?

Examples of graphs in action (p. 333)

• Road map of Arizona
• ``data flow diagram'' for state auto licensing office
• ``star topology'' for network
• neural network
• Graph of ``connectivity'' of rabies-infected towns in Connecticut. (from this rabies presentation). We'll talk about ``adjacency matrices'' next time.

To do: Practice #2, p. 332.

Graph Terminology

To do: Create a graph on a 4x6 card. Some of you should make rather ordered graphs; others might think of very strange graphs.

Graph terminology handout

To do: Practice #3, p. 336.

Special Graphs

By we will understand the simple, complete graph with n nodes.

To do: Practice #4, p. 336. Draw .

A bipartite complete graph is a graph of N nodes which break into two groups, and , of size m and n respecively, with the following property:

two nodes x and y are adjacent and .

To do: Practice #5, p. 337. Draw .

Isomorphic Graphs

The idea of isomorphism is that two structures can be ``morphed'' into each other (they are in some sense identical). Our objective, in general, is to figure out the ``morphism'' (isomorphism - same form!).

To do: Look at Figure 5.17, p. 339: can you morph the two graphs together?

Definition: Two graphs and are isomorphic if there are bijections (one-to-one and onto mappings) and such that for each arc , (replace braces by parentheses for a directed graph).

To do: Practice #7, p. 339. If you managed to morph the two graphs in Figure 5.17, then you should be able to ``see'' the rest of function .

Theorem: Two simple graphs and are isomorphic if there is a bijection such that for any nodes and of , and are adjacent and are adjacent.

To do: Practice #8, p. 340.

There are some tests for determining when two graphs are not isomorphic:

1. The graphs don't have the same number of nodes.
2. The graphs don't have the same number of arcs.
3. One graph is connected and the other isn't.
4. One graph has a node of degree k and the other doesn't.
5. One graph has parallel arcs and the other doesn't.
6. One graph has loops and the other doesn't.
7. One graph has cycles and the other doesn't.

This list is not complete, however: sometimes things get trickier than this (as shown in Example 12).

To do: Practice #9, p. 340.