Section 5.3: Decision Trees

Abstract:

Decision trees are defined, and some examples given.

Decision Tree Definition and Terminology

Definition: a decision tree is a tree in which

• internal nodes represent actions,
• arcs represent outcomes of an action, and
• leaves represent final outcomes.

Examples of decision trees in action

• Figure 5.50, p. 380: Results of tossing a coin 5 times (binary tree)
• Figure 5.51, p. 381: Sequential Search on 5 elements (binary tree)
• Figure 5.52, p. 382: Binary Search (ternary tree)
• Figure 5.55, p. 387: Sorting a list (binary tree, provided distinct list elements)

Exercise #2, p. 388.

Exercise #4, p. 388.

Lower Bounds on Searching

In particular about binary trees:

1. Any binary tree of depth d has at most 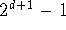nodes. (Proof: look at the full binary tree, as it has the most nodes per depth.)
2. Any binary tree with m nodes has depth .

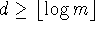The proof of the latter is by contradiction and interesting (p. 384):

• Assume 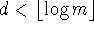: then .
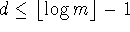• From fact 1, .

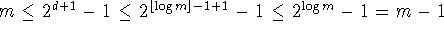By contradiction, 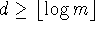. These facts lead to the following

Theorem (on the lower bound for searching):

Any algorithm that solves the search problem for an n-element list by comparing the target element x to the list items must do at least 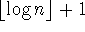comparisons in the worst case.

If, in its worst case, an algorithm does at most this lower bound on worst case behavior is an optimal algorithm in its worst-case behavior.

Binary Search Tree

The Binary search algorithm required a sorted list; if your data is unsorted (it may be changing dynamically in time, if you are updating a database of customers, for example), you can populate a tree which approximates a sorted list, and then use a modified search algorithm (binary tree search) to search the list. A binary search tree is constructed as follows:

• The first item in the list is the root;
• Successive items are inserted by comparing them to existing nodes, from the root node: if less than a node, descend to the left child and iterate; if greater than, descend to the right child.
• If, in descending, there is no child, you create a new node.

Practice #25, p. 386.

The binary tree search algorithm works in the same way as you'd introduce a new node, only the algorithm terminates if

• the element is equal to a node, or
• the element is unequal to a leaf of the binary search tree.

In this case the binary search tree serves as the decision tree for the binary tree search algorithm.

Exercise #9, p. 389.

Sorting

Examine Figure 5.55, p. 387. In this case, we're sorting a three-element list using a decision tree. The author calls this a stupid algorithm (actually, ``not particularly astute''): why?

Practice #26, p. 387.

Assuming no equal elements in the list, then this is indeed a binary (rather than ternary tree, with = included). In this case, we can also get a lower bound on sorting a list with n elements:

• There are n! possible sorted lists, and there are at least that many leaves p ( 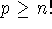). (In Figure 5.55, there are eight leaves, but only 6=3! different sorted lists).
• A worst-case final outcome in the decision tree is given by the depth d of the tree.
• Since the tree is binary, 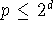(the maximum number of leaves possible at depth d).
• Taking logs (base 2), we get 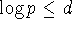, or .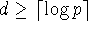
• Hence, .

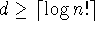This is the Theorem on the lower bound for sorting: that you have to go to at least a depth of 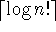in the worst case.