Overview of Chapters 5, 6, and a smidgen of 7 (7.2)
Abstract:
Your test will resemble the problems from your homework assignments.
You will probably have 7 equally weighted questions or so (one every ten
minutes!), one of which will involve several true/false questions (like
the self-tests at the end of each chapter - answers are at the end of the
book).
-
tree: an acyclic, connected graph with one node designated as the
root node (or defined recursively).
-
tree terminology
-
examples of trees
-
tree representations
-
tree traversal algorithms:

-
decision tree: a tree in which
-
internal nodes represent actions,
-
arcs represent outcomes of an action, and
-
leaves represent final outcomes.
-
Examples
-
Lower Bounds on Searching
-
Binary Search Tree (Binary Tree Search)
-
Sorting
-
Theorem on the lower bound for sorting: you have to go to at
least a depth of
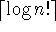 in the worst case.
in the worst case.
-
Euler Path: a path in which each arc is used exactly once.
-
Theorem: in any graph, the number of odd nodes (nodes of odd degree) is
even.
-
Theorem: an Euler path exists in a connected graph
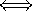 there are
either two or zero odd nodes.
there are
either two or zero odd nodes. -
Using the EulerPath algorithm (simply counts up elements in a row i of
the matrix (the degree of node i), and checks whether that's even or odd; if
in the end there are not zero or two even nodes, there's no Euler path!)
-
Hamiltonian Circuit: a cycle using every node of the graph.
-
Shortest Path algorithms (for a simple,
positively weighted, connected graph)
-
Dijkstra's Algorithm
-
Bellman-Ford Algorithm
-
Floyd's algorithm
-
Minimal Spanning Trees:
A spanning tree for a connected graph G is a non-rooted tree
containing the nodes of the graph and a subset of the arcs of G.
A minimal spanning tree is a spanning tree of least weight of a simple,
weighted, connected graph G.
-
Prim's algorithm
-
Kruskal's algorithm
Traversing a graph (generalizes tree traversal):
-
depth-first strategy
-
breadth-first strategy
Remember: for the test stick with the convention that, given a choice,
we should choose nodes in alphabetic order.
Remember that we are skipping section 7.1, at democratic request, and replacing
that with section 7.2. Hence you will be expected to know the properties of a
Boolean algebra, but will not be called upon to prove anything about Boolean
algebras.
-
Equivalent representations of a Logic Network:
-
Truth Functions
-
Boolean Expressions
-
Logic Network
-
Converting between the three forms
-
Rudimentary simplification of Boolean expressions
-
Adding binary numbers (as Boolean expressions, half-adder, full-adder)
LONG ANDREW E
Tue Apr 9 18:56:23 EDT 2002
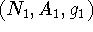 and
and 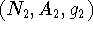 are
isomorphic if there are bijections (one-to-one and onto mappings)
are
isomorphic if there are bijections (one-to-one and onto mappings)
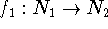 and
and 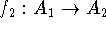 such that for each arc
such that for each arc 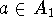 ,
,
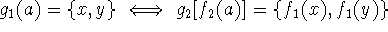 (replace braces by
parentheses for a directed graph).
(replace braces by
parentheses for a directed graph).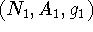 and
and 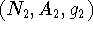 are
isomorphic if there is a bijection
are
isomorphic if there is a bijection 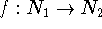 such that for any nodes
such that for any nodes
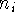 and
and 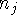 of
of 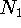 ,
, 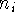 and
and 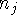 are adjacent
are adjacent 
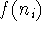 and
and
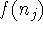 are adjacent.
are adjacent.![]()
