where
We model a machine as a set of states, inputs which lead to a change in state, a clock to synchronize the machine world, and outputs, which result from a particular state. We use tables and graphs to describe how the inputs relate to changes in state and the outputs of each state, then practice creating simple finite-state machines.
Definition: A finite-state machine M is a structure
where
Table: Elements of a finite-state machine.
We assume discrete times, synchronized by a clock, so that
and that
We represent 
and 
by
Let's practice identifying these elements with the aid of Example 16, p. 559.
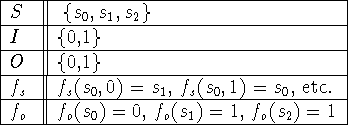
Table: Elements of finite-state machine of Example 16, p. 559.
Practice 36, p. 561. (First of all: what are in the
example?)
Practice 35, p. 561. (Table from graph)
Practice 34, p. 561.
Note: major goof - the fourth sum at the bottom of page 561 is wrong - yikes! We know that 0+1=1, while 1+1=10 in binary....
In section 7.2 we saw how one might create a logic network in hardware for the addition of binary numbers. We now consider how this can be incorporated into a finite-state machine which is analogous (p. 561).
We must specify the five elements of a finite-state machine: .
What is the set of states, what the set of inputs, what the set of outputs, and
how are the functions and defined?
Practice 37, p. 562
Practice 38, p. 563
Exercise 13(a), p. 578