Overview of Chapters 7.1, 7.3 and 8.2

Abstract:

Since these sections are new, you will be expected to do some problems from these sections. You will also be expected to do some problems from previous material. Since you have two hours, I imagine that I might give you 11 problems, and allow you to skip one.

As I mentioned in class, there are some topics from earlier days which I would have liked to have tested you over, but which didn't make the first cut. I may go back to those topics. (For example, we didn't do an example of graph isomorphism on the test - I was itching to do one of those!). So you might be on the lookout for topics which didn't appear on the first or second tests, but which were emphasized in the problems and in class.

On the other hand, you can expect to see problems similar to those you encountered on the homework. No real ringers should be expected.

Section 7.1

Definition: a Boolean Algebra is a set B on which are defined two binary operations + and , and one unary operation ', and in which there are two distinct elements 0 and 1 such that the following properties hold for all :

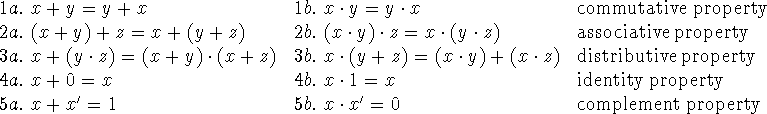
The element x' is called the complement of x. The algebra may be denoted .

For proofs, you will want to remember

• idempotence
• duality (only need to show half - the other half you get for free by symmetry!)
• for small Boolean algebras, you can demonstrate the properties exhaustively (that is, simply show that the properties are true for all the elements).
• Usually the best approach is to start with the more complicated expression and try to show that it reduces to the simpler expression.
• Think of adding some form of 0 (like ) or multiplying by some form of 1 (like x+x').
• Don't forget property 3a, the distributive property of addition over multiplication, just because it seems weird!
• don't forget to consider the problem in some familiar context (like propositional logic) to see if it makes sense!). One nice problem is always to ask the student to either prove that a statement or theorem is true, or show that it's false!

Section 7.3

While section 7.3 included two methods of simplification, we only studies the Karnaugh map in depth. Hence, only it will be included on the test.

Remember how the Karnaugh map uses idempotence to produce multiple copies of elements for the matches (pairs, quads, etc.), which it then can simplify.

Remember that you may use the techniques of the Karnaugh map to produce different simplified Boolean expressions: make sure that you've made things as simple as possible, but not simpler! (You can always check your Boolean expressions to make sure that they are equal by using the original ``tuples'' in the simplified expressions, and you should get 1!

Section 8.2

Definition: A finite-state machine M is a structure where

  
Table: Elements of a finite-state machine.

Construction of finite-state machines to perform tasks

• the binary adder, for example
• set recognition.

Given a machine, determine whether a set is recognized by it or not. Or determine what set is recognized by it. Remember that machine recognition is defined as follows, with emphasis on the word ``ends'' below:

Definition: Finite-State Machine Recognition A finite-state machine M with input alphabet I recognizes a subset S of (the set of finite-length strings over the input alphabet I) if M, beginning in state and processing an input string , ends in a final state (a state with output 1) if and only if .

Regular expressions define sets of input strings which are the ones that finite-state machines can actually recognize. The existence of reasonable sets, which one should reasonably be able to detect (e.g. , where stands for n copies of a), finite-state machines are obviously not sufficient to understand all of computation.

The essential failure is related to memory: the finite-state machine cannot do what the Turing machine does, which is reread input and overwrite it (unlimited memory)! These are the essential elements missing from the finite-state machine which reduce its utility.